设A是正规矩阵 证明: (1)A的特征向量也是AH的特征向量; (2)AX与AHX的长度相等.请帮忙
设A是正规矩阵,证明: (1)A的特征向量也是AH的特征向量; (2)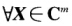 AX与AHX的长度相等.
AX与AHX的长度相等.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)A为正规矩阵则有酉矩阵使得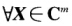 其中U=(α1α2…αn)α1α2…αn为A的特征向量由上两式可知Aα1=λα: AHαi=λiαi故A和AH有相同的特征向量. (2)由AHA=AAH得∣AHX∣2=(AHX)HH(AHx)=xHAAHX=XHAHAX=(Ax)H(AX)=∣AX∣2所以∣AHX∣=∣AX∣.
其中U=(α1α2…αn)α1α2…αn为A的特征向量由上两式可知Aα1=λα: AHαi=λiαi故A和AH有相同的特征向量. (2)由AHA=AAH得∣AHX∣2=(AHX)HH(AHx)=xHAAHX=XHAHAX=(Ax)H(AX)=∣AX∣2所以∣AHX∣=∣AX∣.
(1)A为正规矩阵,则有酉矩阵,使得其中U=(α1,α2,…,αn),α1,α2,…,αn为A的特征向量,由上两式可知Aα1=λα:AHαi=λiαi,故A和AH有相同的特征向量.(2)由AHA=AAH,得∣AHX∣2=(AHX)HH(AHx)=xHAAHX=XHAHAX=(Ax)H(AX)=∣AX∣2所以∣AHX∣=∣AX∣.
相似问题
设∥x∥是Pn中的向量范数 A∈Pn×n 则∥Ax∥也是Pn中的向量范数的充要条件为A是可逆矩阵.请
设∥x∥是Pn中的向量范数,A∈Pn×n,则∥Ax∥也是Pn中的向量范数的充要条件为A是可逆矩阵.请帮忙给出正确答案和分析,谢谢!
证明:方程组AHAx=AHb是相容的 其中A∈Cm×n b∈Cm.请帮忙给出正确答案和分析 谢谢!
证明:方程组AHAx=AHb是相容的,其中A∈Cm×n,b∈Cm.请帮忙给出正确答案和分析,谢谢!
设A2=A=AH 试证明:A=A+.请帮忙给出正确答案和分析 谢谢!
设A2=A=AH,试证明:A=A+.请帮忙给出正确答案和分析,谢谢!
设A∈Cm×n D G∈A{1} 试证明:GAD∈A{1 2).请帮忙给出正确答案和分析 谢谢!
设A∈Cm×n,D,G∈A{1},试证明:GAD∈A{1,2).请帮忙给出正确答案和分析,谢谢!
设X∈Rn×n det(X)≠0 f(X)=det(X).证明请帮忙给出正确答案和分析 谢谢!
设X∈Rn×n,det(X)≠0,f(X)=det(X).证明请帮忙给出正确答案和分析,谢谢!












