设W1 w2为线性空间V的两个子空间 令W1∩W2={X∣X∈W1 且X∈W2} W1∪W2={X∣

正确答案：(1)W₁∩W₂是V的子空间证明如下因W₁W₀为V的线性子空间均含有零元因而W₁∩W₂是非空集再假定αβ∈W₁∩W₂则αβ∈W₁αβ∈W₂因W₁W₂为子空间故α+β∈W₁α+β∈W₂于是α+β∈W₁∩W₂．同样因λ_α∈W₁λ_α∈W₂故λ_α∈W₁∩W₂因而W₁∩W₂是V的子空间． (2)W₁∪W₂不一定是V的子空间．反例如下．取V=R₂令W₁={(x0)_Tx∈R W₂={(0y)_T∣y∈R则它们均为R₂的子空间取α=(10)_Tβ=(01)_T显然αβ∈W₁∪W₂但α+β=(10)_T+(01)_T=(11)_T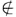W₁∪W₂因而W₁∪W₂不是R₂的子空间． 注 本题第二部分实际上对任意有限个子空间也是成立的即若W₁W₂…W_s为线性空间V的s个非平凡子空间则V中至少有一个向量不属于W₁W₂…W_s中任何一个．
(1)W1∩W2是V的子空间,证明如下,因W1,W0为V的线性子空间,均含有零元,因而W1∩W2是非空集再假定α,β∈W1∩W2,则α,β∈W1,α,β∈W2因W1,W2为子空间,故α+β∈W1,α+β∈W2,于是α+β∈W1∩W2．同样,因λα∈W1λα∈W2,故λα∈W1∩W2,因而W1∩W2是V的子空间．(2)W1∪W2不一定是V的子空间．反例如下．取V=R2,令W1={(x,0)Tx∈R,W2={(0,y)T∣y∈R,则它们均为R2的子空间,取α=(1,0)T,β=(0,1)T,显然α,β∈W1∪W2,但α+β=(1,0)T+(0,1)T=(1,1)TW1∪W2,因而W1∪W2不是R2的子空间．注本题第二部分实际上对任意有限个子空间也是成立的,即若W1,W2,…,Ws为线性空间V的s个非平凡子空间,则V中至少有一个向量不属于W1,W2,…,Ws中任何一个．