设A为正规矩阵 则A的谱分解式有A=λ1U1U1H+λ2U2U2H+…+λnUnUnH 其中U1U2
设A为正规矩阵，则A的谱分解式有A=λ1U1U1H+λ2U2U2H+…+λnUnUnH，其中U1U2，…，Un是A的n个特征值λ1λ2，…，λn对应的标准正交特征向量．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***101
2024-11-11 19:43:59
正确答案：A是正规矩阵则存在酉矩阵U使得
把U列分块为U=(U1 U2 … Un)则A=(U1 U2 … Un)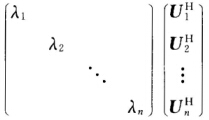
=λ1U11H+λ2U2U2H+…+λnUnUnH
A是正规矩阵,则存在酉矩阵U,使得把U列分块为U=(U1U2…Un),则A=(U1U2…Un)=λ1U11H+λ2U2U2H+…+λnUnUnH
相似问题
设∥A∥a是Cn×n上的相容矩阵范数 B C都是n阶可逆矩阵 且∥B－1∥a及∥C－1∥a都小于或等
设∥A∥a是Cn×n上的相容矩阵范数，B，C都是n阶可逆矩阵，且∥B－1∥a及∥C－1∥a都小于或等于1，证明对任何A∈Cn×n，∥A∥b=∥BAC∥a定义了Cn×n上的一
设A∈Cn×n 证明： 请帮忙给出正确答案和分析 谢谢！
设A∈Cn×n，证明： 请帮忙给出正确答案和分析，谢谢！
设实对称阵A和B的特征值分别是λ1≤λ2≤…≤λn和u1≤u2≤…≤un 若对单位向量x 恒有∣xT
设实对称阵A和B的特征值分别是λ1≤λ2≤…≤λn和u1≤u2≤…≤un，若对单位向量x，恒有∣xT(B－A)x∣≤ε(ε>0)，则∣uk=λk∣≤ε(k=1，2，…，n)．请
设A∈Cn×n是非奇异矩阵 那么A1相似于A*当且仅当存在非奇异矩阵B∈Cn×n 使得A=B1B*．
设A∈Cn×n是非奇异矩阵，那么A1相似于A*当且仅当存在非奇异矩阵B∈Cn×n，使得A=B1B*．请帮忙给出正确答案和分析，谢谢！
证明：对于R1中的任何向量范数∥x∥ 一定有∥x∥=λ∣x∣ 其中λ>0．请帮忙给出正确答案和分析
证明：对于R1中的任何向量范数∥x∥，一定有∥x∥=λ∣x∣，其中λ>0．请帮忙给出正确答案和分析，谢谢！
