设两条曲率大于0的C2曲线之间可建立(可微的)一一对应 使对应点切线处处相同.问:两曲线重合吗?请帮
设两条曲率大于0的C2曲线之间可建立(可微的)一一对应,使对应点切线处处相同.问:两曲线重合吗?
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:设一条曲线为x(s)(s为其弧长)则另一条曲线记为x(s)一x(s)+λ(s)V1(s)其中S为其参数但未必为其弧长.于是根据题意有x'(s)=x'(s)+λ'(s)V1(s)+λ(s)V1'(s)=[1+λ'(s)V1(s)+λ(s)x(s)V2(s)λ(s)k(s)=0.因为x>0故λ(s)=0从而x(s)=x(s)即得两曲线重合.注如果曲率大于0的条件删去则讨论如下:(1)如果恒有k(s)>0则λ(s)≡0从而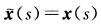 即两曲线
即两曲线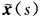 与x(s)重合.(2)如果F={s|k(s)=0)不含区间则两曲线
与x(s)重合.(2)如果F={s|k(s)=0)不含区间则两曲线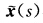 与x(s)重合.事实上由k(s)连续性知G={s|k(s)>0为直线上的开集根据(1)λ(s)=0s∈G.故两曲线
与x(s)重合.事实上由k(s)连续性知G={s|k(s)>0为直线上的开集根据(1)λ(s)=0s∈G.故两曲线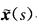 与x(s)在G上重合即
与x(s)在G上重合即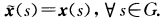 .再由于F={s|k(s)=0)不含区间故G={s|k(s)≥0.根据
.再由于F={s|k(s)=0)不含区间故G={s|k(s)≥0.根据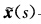 与x(s)的连续性有
与x(s)的连续性有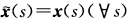 即两曲线
即两曲线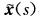 与x(s)重合.(3)如果F={s|k(s)=0)含闭区间
与x(s)重合.(3)如果F={s|k(s)=0)含闭区间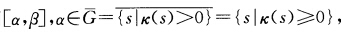
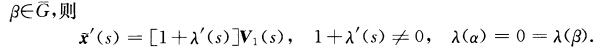 此时由k(s)=0s∈αβ并根据引理1.2.2x(s)限制在[αβ上为直线段V1(s)=x'(s)为常单位向量它是该直线段的方向向量.由于λ(s)≠0(α≤s≤β故
此时由k(s)=0s∈αβ并根据引理1.2.2x(s)限制在[αβ上为直线段V1(s)=x'(s)为常单位向量它是该直线段的方向向量.由于λ(s)≠0(α≤s≤β故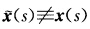 (α
(α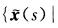 s∈[αβ)与{x(s)|s∈[αβ))为同一切线上的线段.当λ(s)≠0(特别当λ(s)>0)时点集
s∈[αβ)与{x(s)|s∈[αβ))为同一切线上的线段.当λ(s)≠0(特别当λ(s)>0)时点集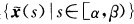 与{x(s)|s∈[αβ))未必相同.类似参考文献[7第38页引理1构造R上的C∞函数λ(s)使得λ'(s)≥0且
与{x(s)|s∈[αβ))未必相同.类似参考文献[7第38页引理1构造R上的C∞函数λ(s)使得λ'(s)≥0且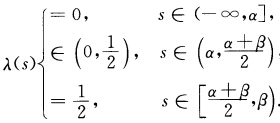 此时点集
此时点集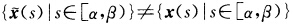 ;显然也有
;显然也有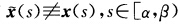 .同样对F含半开半闭区间(αβ的情形有类似的上述结果.(5)当F={s|k(s)=0)=R或F含(一∞α或F含[α+∞)时类似于(4)的讨论并有类似的结论.
.同样对F含半开半闭区间(αβ的情形有类似的上述结果.(5)当F={s|k(s)=0)=R或F含(一∞α或F含[α+∞)时类似于(4)的讨论并有类似的结论.
设一条曲线为x(s)(s为其弧长),则另一条曲线记为x(s)一x(s)+λ(s)V1(s),其中S为其参数,但未必为其弧长.于是,根据题意,有x'(s)=x'(s)+λ'(s)V1(s)+λ(s)V1'(s)=[1+λ'(s)V1(s)+λ(s)x(s)V2(s),λ(s)k(s)=0.因为x>0,故λ(s)=0,从而x(s)=x(s),即得两曲线重合.注如果曲率大于0的条件删去,则讨论如下:(1)如果恒有k(s)>0,则λ(s)≡0,从而,即两曲线与x(s)重合.(2)如果F={s|k(s)=0)不含区间,则两曲线与x(s)重合.事实上,由k(s)连续性知,G={s|k(s)>0为直线上的开集,根据(1),λ(s)=0,s∈G.故两曲线与x(s)在G上重合,即.再由于F={s|k(s)=0)不含区间,故G={s|k(s)≥0.根据与x(s)的连续性,有,即两曲线与x(s)重合.(3)如果F={s|k(s)=0)含闭区间此时,由k(s)=0,s∈α,β,并根据引理1.2.2,x(s)限制在[α,β上为直线段,V1(s)=x'(s)为常单位向量,它是该直线段的方向向量.由于λ(s)≠0(α≤s≤β,故(α,则点集s∈[α,β)与{x(s)|s∈[α,β))为同一切线上的线段.当λ(s)≠0(特别当λ(s)>0)时,点集与{x(s)|s∈[α,β))未必相同.类似参考文献[7第38页引理1,构造R上的C∞函数λ(s),使得λ'(s)≥0,且此时,点集;显然,也有.同样,对F含半开半闭区间(α,β的情形,有类似的上述结果.(5)当F={s|k(s)=0)=R或F含(一∞,α或F含[α,+∞)时,类似于(4)的讨论,并有类似的结论.
相似问题
证明:当R3中曲面M的参数曲线取曲率线网时 Codazzi方程化为Lv=HEv Nu=HGu.从而再
证明:当R3中曲面M的参数曲线取曲率线网时,Codazzi方程化为Lv=HEv,Nu=HGu.从而再证明:平均曲率为常数的连通曲面为平面片,或者为球面片,或者第1、第
设曲面M:x(u v)=(ucosv usinv lnu)与设M为R3中2维光滑曲面 {u v}为点
设曲面M:x(u,v)=(ucosv,usinv,lnu)与设M为R3中2维光滑曲面,{u,v}为点P∈M邻近的局部坐标(参数),{x设M为R3中2维光滑曲面,{u,v}为点P∈M邻近的局
证明:(1)证明:正螺面M:x(u v)=(vcosu vsinu bu) (0≤u≤2π 一∞
证明:(1)证明:正螺面M:x(u,v)=(vcosu,vsinu,bu) (0≤u≤2π,一∞<v<+∞)的渐近曲线就是它上面证明:正螺面M:x(u,v)=(vcosu,vsinu,bu) (0≤
若曲面M:x(u v)在某一参数(u v)下 xuu=0=xuv 证明:曲面M为柱面.请帮忙给出正确
若曲面M:x(u,v)在某一参数(u,v)下,xuu=0=xuv,证明:曲面M为柱面.请帮忙给出正确答案和分析,谢谢!
若连通曲面M在某一参数表示下 E F G L M N均为常数 证明:曲面M为平面或圆柱面.请帮忙给出
若连通曲面M在某一参数表示下,E,F,G,L,M,N均为常数,证明:曲面M为平面或圆柱面.请帮忙给出正确答案和分析,谢谢!












