设曲面M:x(u v)=(ucosv usinv lnu)与设M为R3中2维光滑曲面 {u v}为点
设曲面M:x(u,v)=(ucosv,usinv,lnu)与设M为R3中2维光滑曲面,{u,v}为点P∈M邻近的局部坐标(参数),{x
设M为R3中2维光滑曲面,{u,v}为点P∈M邻近的局部坐标(参数),{x(u,v),xu(u,v),xv(u,v),n(u,v)}称为自然标架场.{x(u,v),e1(u,v),e 2(u,v),e3(u,v))为规范正交标架场,dx,dei(i=1,2,3)都可用e1,e2,e3的线性组合表示.此公式称为曲面M的基本公式(或运动方程):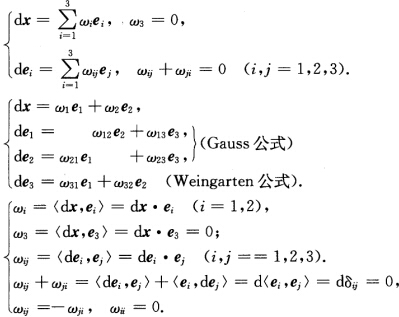 在近代微分几何中,R3中的光滑曲面M:x=x(u,v),它的自然切标架场为{xu,xv),并称{du,dv}为它的对偶余切标架场,即du(xu)=1, du(xv)=0,dv(xu)=0, dv(xv)=1.而{e1,e2,e2}为R3中的规范正交活动标架,它限制到曲面M上,{e1,e2}为M上的规范正交切标架场,e3为M的法标架场,{ω1,ω2,ω3}为{e1,e2,e3}的对偶标架场,即ωi(ej)=δij (i,j=1,2,3).曲面M的第1和第2基本形式分别为
在近代微分几何中,R3中的光滑曲面M:x=x(u,v),它的自然切标架场为{xu,xv),并称{du,dv}为它的对偶余切标架场,即du(xu)=1, du(xv)=0,dv(xu)=0, dv(xv)=1.而{e1,e2,e2}为R3中的规范正交活动标架,它限制到曲面M上,{e1,e2}为M上的规范正交切标架场,e3为M的法标架场,{ω1,ω2,ω3}为{e1,e2,e3}的对偶标架场,即ωi(ej)=δij (i,j=1,2,3).曲面M的第1和第2基本形式分别为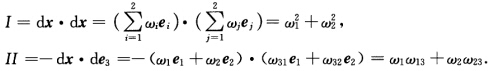 定理1如果{u,v}为曲面M的正交坐标系,则有下面的计算公式:
定理1如果{u,v}为曲面M的正交坐标系,则有下面的计算公式: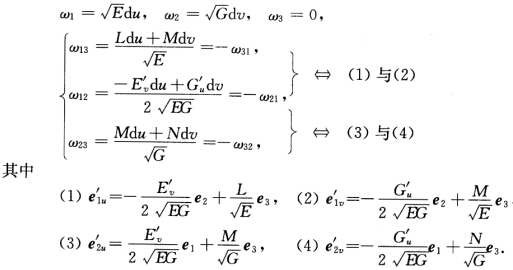
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:因为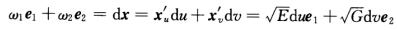 所以
所以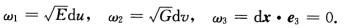 又因为
又因为 所以
所以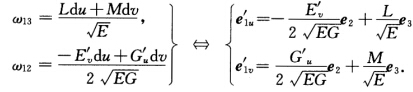 同理因为
同理因为 所以
所以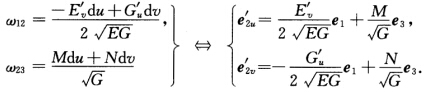 定理2 R3中曲面的基本方程(结构方程):设曲面M的基本公式中的度量形式ωi及联络形式ωij满足:(1)第1结构方程:
定理2 R3中曲面的基本方程(结构方程):设曲面M的基本公式中的度量形式ωi及联络形式ωij满足:(1)第1结构方程: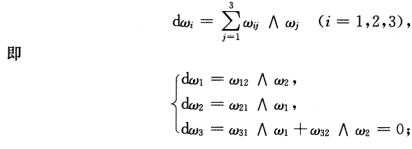 (2)第2结构方程:
(2)第2结构方程: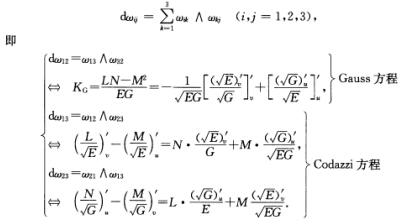 证明 (1)设{uv为正交坐标.因为
证明 (1)设{uv为正交坐标.因为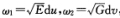 所以
所以
 (←)由注2.9.3得.(→)由例2.11.2得.类似上面的证明或者根据对称性有
(←)由注2.9.3得.(→)由例2.11.2得.类似上面的证明或者根据对称性有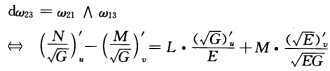 (←)由注2.9.3得.(→)由例2.11.2得.
(←)由注2.9.3得.(→)由例2.11.2得.
因为所以又因为所以同理,因为所以定理2R3中曲面的基本方程(结构方程):设曲面M的基本公式中的度量形式ωi及联络形式ωij满足:(1)第1结构方程:(2)第2结构方程:证明(1)设{u,v为正交坐标.因为,所以(←)由注2.9.3得.(→)由例2.11.2得.类似上面的证明,或者根据对称性,有(←)由注2.9.3得.(→)由例2.11.2得.
相似问题
证明:(1)证明:正螺面M:x(u v)=(vcosu vsinu bu) (0≤u≤2π 一∞
证明:(1)证明:正螺面M:x(u,v)=(vcosu,vsinu,bu) (0≤u≤2π,一∞<v<+∞)的渐近曲线就是它上面证明:正螺面M:x(u,v)=(vcosu,vsinu,bu) (0≤
若曲面M:x(u v)在某一参数(u v)下 xuu=0=xuv 证明:曲面M为柱面.请帮忙给出正确
若曲面M:x(u,v)在某一参数(u,v)下,xuu=0=xuv,证明:曲面M为柱面.请帮忙给出正确答案和分析,谢谢!
若连通曲面M在某一参数表示下 E F G L M N均为常数 证明:曲面M为平面或圆柱面.请帮忙给出
若连通曲面M在某一参数表示下,E,F,G,L,M,N均为常数,证明:曲面M为平面或圆柱面.请帮忙给出正确答案和分析,谢谢!
证明:曲面M:x(x y)=(x y f(x y))的第1 第2基本形式分别为证明:面积与曲面参数的
证明:曲面M:x(x,y)=(x,y,f(x,y))的第1、第2基本形式分别为证明:面积与曲面参数的选取无关(参阅定证明:面积与曲面参数的选取无关(参阅定理2.3.1
若平移曲面M:x(u v)=a(u)+b(v)的参数曲线构成正交网 证明:M必为柱面.请帮忙给出正确
若平移曲面M:x(u,v)=a(u)+b(v)的参数曲线构成正交网,证明:M必为柱面.请帮忙给出正确答案和分析,谢谢!












