证明:当R3中曲面M的参数曲线取曲率线网时 Codazzi方程化为Lv=HEv Nu=HGu.从而再
证明:当R3中曲面M的参数曲线取曲率线网时,Codazzi方程化为Lv=HEv,Nu=HGu.从而再证明:平均曲率为常数的连通曲面为平面片,或者为球面片,或者第1、第2基本形式由下式给出:Ⅰ=λ(du-2+dv-2)Ⅱ=(1+λH)du-2-(1-λH)dv-2
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)将定理2.5.6证明中的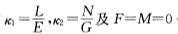 代入习题2.9.1中的
代入习题2.9.1中的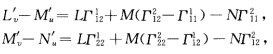 得到
得到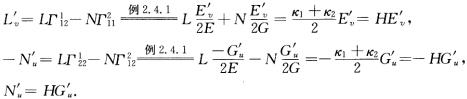 (2)当H=常数时由Lv'=HEv'Nu'=HGu'推得L=HE+φ(u) N=HG+ψ(v).从而有
(2)当H=常数时由Lv'=HEv'Nu'=HGu'推得L=HE+φ(u) N=HG+ψ(v).从而有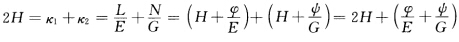 所以
所以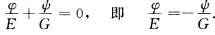 情况1设上式为0即φ=ψ=0L=HEN=HG注意到M=F=0有 (LMN)=H(EFG).因此曲面是全脐的根据引理3.1.4(1)连通曲面M或为平面片或为球面片.情况2 当上式中
情况1设上式为0即φ=ψ=0L=HEN=HG注意到M=F=0有 (LMN)=H(EFG).因此曲面是全脐的根据引理3.1.4(1)连通曲面M或为平面片或为球面片.情况2 当上式中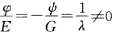 时有E=λφG=一λψ.从而有L=(1+λH)ψN=(1一λH)ψ.(a)若λ>0时有
时有E=λφG=一λψ.从而有L=(1+λH)ψN=(1一λH)ψ.(a)若λ>0时有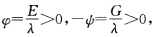 作变换
作变换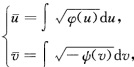 则
则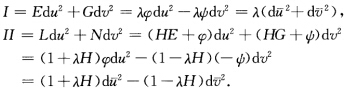 (b)若λ<0时
(b)若λ<0时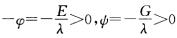 作变换
作变换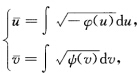 则
则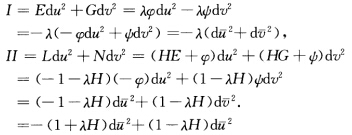 如果交换
如果交换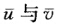 并用一λ代λ则Ⅰ与Ⅱ分别为
并用一λ代λ则Ⅰ与Ⅱ分别为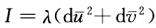
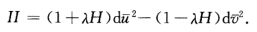 情况3当上式中
情况3当上式中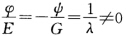 时可能有
时可能有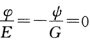 未能讨论清.
未能讨论清.
(1)将定理2.5.6证明中的代入习题2.9.1中的得到(2)当H=常数时,由Lv'=HEv',Nu'=HGu',推得L=HE+φ(u),N=HG+ψ(v).从而有所以情况1设上式为0,即φ=ψ=0,L=HE,N=HG,注意到M=F=0,有(L,M,N)=H(E,F,G).因此,曲面是全脐的,根据引理3.1.4(1),连通曲面M或为平面片,或为球面片.情况2当上式中时,有E=λφ,G=一λψ.从而有L=(1+λH)ψ,N=(1一λH)ψ.(a)若λ>0时,有作变换则(b)若λ<0时,作变换则如果交换,并用一λ代λ,则Ⅰ与Ⅱ分别为,情况3当上式中时,可能有未能讨论清.
相似问题
设曲面M:x(u v)=(ucosv usinv lnu)与设M为R3中2维光滑曲面 {u v}为点
设曲面M:x(u,v)=(ucosv,usinv,lnu)与设M为R3中2维光滑曲面,{u,v}为点P∈M邻近的局部坐标(参数),{x设M为R3中2维光滑曲面,{u,v}为点P∈M邻近的局
证明:(1)证明:正螺面M:x(u v)=(vcosu vsinu bu) (0≤u≤2π 一∞
证明:(1)证明:正螺面M:x(u,v)=(vcosu,vsinu,bu) (0≤u≤2π,一∞<v<+∞)的渐近曲线就是它上面证明:正螺面M:x(u,v)=(vcosu,vsinu,bu) (0≤
若曲面M:x(u v)在某一参数(u v)下 xuu=0=xuv 证明:曲面M为柱面.请帮忙给出正确
若曲面M:x(u,v)在某一参数(u,v)下,xuu=0=xuv,证明:曲面M为柱面.请帮忙给出正确答案和分析,谢谢!
若连通曲面M在某一参数表示下 E F G L M N均为常数 证明:曲面M为平面或圆柱面.请帮忙给出
若连通曲面M在某一参数表示下,E,F,G,L,M,N均为常数,证明:曲面M为平面或圆柱面.请帮忙给出正确答案和分析,谢谢!
证明:曲面M:x(x y)=(x y f(x y))的第1 第2基本形式分别为证明:面积与曲面参数的
证明:曲面M:x(x,y)=(x,y,f(x,y))的第1、第2基本形式分别为证明:面积与曲面参数的选取无关(参阅定证明:面积与曲面参数的选取无关(参阅定理2.3.1












