若连通曲面M在某一参数表示下 E F G L M N均为常数 证明:曲面M为平面或圆柱面.请帮忙给出
若连通曲面M在某一参数表示下,E,F,G,L,M,N均为常数,证明:曲面M为平面或圆柱面.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由于第1基本形式的系数构成正定矩阵根据线性代数中二次型理论可通过坐标的正交常系数线性变换将I=Edu2+2Fdudv+Gdv2与Ⅱ=Ldu2+2Mdudv+Ndv2同时化为对角形: 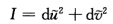 与
与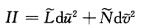 (以下仍将
(以下仍将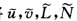 记为uvLN).与习题2.7.10和习题2.7.12一样可证得LN=KG=0. (a)常数L≠0N=0.由KG=0和例2.7.7曲面M是可展的.设M:x(uv)=a(u)+vl(u)l2(u)=1l'(u).l(u)=0a'(u).l(u)=0 a'(u)2=1.xu'.xv'=[a'(u)+vl'(u).l(u)=a'(u).l(u)+vl'(u).l(u)=0?由OlinderR0drigues公式(定理2.5.4(2))知
记为uvLN).与习题2.7.10和习题2.7.12一样可证得LN=KG=0. (a)常数L≠0N=0.由KG=0和例2.7.7曲面M是可展的.设M:x(uv)=a(u)+vl(u)l2(u)=1l'(u).l(u)=0a'(u).l(u)=0 a'(u)2=1.xu'.xv'=[a'(u)+vl'(u).l(u)=a'(u).l(u)+vl'(u).l(u)=0?由OlinderR0drigues公式(定理2.5.4(2))知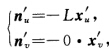 其中L与0为主曲率(由定理2.5.6
其中L与0为主曲率(由定理2.5.6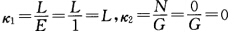 或者k1k2=KG=0则k1=0或k2=0不妨设k2=0.又有k1=k1+0=k1+k2=2H=
或者k1k2=KG=0则k1=0或k2=0不妨设k2=0.又有k1=k1+0=k1+k2=2H=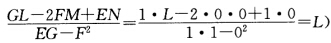 从上面第2式知n与v无关故n=n(u)nu'=一Lxu'=-L[a'(u)+vl'(u).由此推得l'(u)=0l(u)为单位向量.积分nu'=一La'(u)得到n(u)=一La(u)+C(c为常向量).代入
从上面第2式知n与v无关故n=n(u)nu'=一Lxu'=-L[a'(u)+vl'(u).由此推得l'(u)=0l(u)为单位向量.积分nu'=一La'(u)得到n(u)=一La(u)+C(c为常向量).代入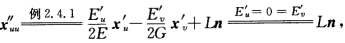 得到 a''=a''+vl''=xuu''=Ln=L(一La+c)=一L2a+Lc.对n(u)作一平移使上述方程化为a''(u)=L2a(u)=0.解此常系数向量2阶微分方程得 a(u)=Tcos Lu+S.sin Lu (TS为常向量).由0=a'(u).l=L(一Tsin Lu+S.cosLu).l=L(一T.lsinLu+S.cos Lu)推得T.l=0 S.l=0即常向量TS都垂直于l.另一方面由1=[a'(u)2=L2(一TsinLu+ScosLu)2=L2(T2sin2Lu一2T.SsincosLu+S2cos2Lu)立知
得到 a''=a''+vl''=xuu''=Ln=L(一La+c)=一L2a+Lc.对n(u)作一平移使上述方程化为a''(u)=L2a(u)=0.解此常系数向量2阶微分方程得 a(u)=Tcos Lu+S.sin Lu (TS为常向量).由0=a'(u).l=L(一Tsin Lu+S.cosLu).l=L(一T.lsinLu+S.cos Lu)推得T.l=0 S.l=0即常向量TS都垂直于l.另一方面由1=[a'(u)2=L2(一TsinLu+ScosLu)2=L2(T2sin2Lu一2T.SsincosLu+S2cos2Lu)立知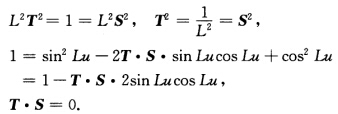 因此
因此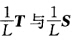 为垂直于固定常单位向量l的平面π上的规范正交基.由此推得a(u)为垂直于l的平面上的圆而x(uv)为以此圆为准线、以固定方向l为母线的圆柱面.(b)常数N≠0L=0.类似(a)可证得M为圆柱面.(c)常数L=N=0.由M=0再根据引理3.1.4知M为平面(片).或者由
为垂直于固定常单位向量l的平面π上的规范正交基.由此推得a(u)为垂直于l的平面上的圆而x(uv)为以此圆为准线、以固定方向l为母线的圆柱面.(b)常数N≠0L=0.类似(a)可证得M为圆柱面.(c)常数L=N=0.由M=0再根据引理3.1.4知M为平面(片).或者由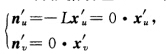 知n(uv)为常单位向量.因此d(xn)=dx.n+x.dn=0+x.0=0x.n=常值即M为连通的平面(片).
知n(uv)为常单位向量.因此d(xn)=dx.n+x.dn=0+x.0=0x.n=常值即M为连通的平面(片).
由于第1基本形式的系数构成正定矩阵,根据线性代数中二次型理论,可通过坐标的正交常系数线性变换,将I=Edu2+2Fdudv+Gdv2与Ⅱ=Ldu2+2Mdudv+Ndv2同时化为对角形:与(以下仍将记为u,v,L,N).与习题2.7.10和习题2.7.12一样,可证得LN=KG=0.(a)常数L≠0,N=0.由KG=0和例2.7.7,曲面M是可展的.设M:x(u,v)=a(u)+vl(u),l2(u)=1,l'(u).l(u)=0,a'(u).l(u)=0,a'(u)2=1.xu'.xv'=[a'(u)+vl'(u).l(u)=a'(u).l(u)+vl'(u).l(u)=0?由OlinderR0drigues公式(定理2.5.4(2))知其中L与0为主曲率(由定理2.5.6,或者k1k2=KG=0,则k1=0或k2=0,不妨设k2=0.又有k1=k1+0=k1+k2=2H=从上面第2式知n与v无关,故n=n(u),nu'=一Lxu'=-L[a'(u)+vl'(u).由此推得l'(u)=0,l(u)为单位向量.积分nu'=一La'(u),得到n(u)=一La(u)+C(c为常向量).代入得到a''=a''+vl''=xuu''=Ln=L(一La+c)=一L2a+Lc.对n(u)作一平移,使上述方程化为a''(u)=L2a(u)=0.解此常系数向量2阶微分方程,得a(u)=TcosLu+S.sinLu,(T,S为常向量).由0=a'(u).l=L(一TsinLu+S.cosLu).l=L(一T.lsinLu+S.cosLu)推得T.l=0,S.l=0,即常向量T,S都垂直于l.另一方面,由1=[a'(u)2=L2(一TsinLu+ScosLu)2=L2(T2sin2Lu一2T.SsincosLu+S2cos2Lu),立知因此,为垂直于固定常单位向量l的平面π上的规范正交基.由此推得a(u)为垂直于l的平面上的圆,而x(u,v)为以此圆为准线、以固定方向l为母线的圆柱面.(b)常数N≠0,L=0.类似(a)可证得M为圆柱面.(c)常数L=N=0.由M=0,再根据引理3.1.4知M为平面(片).或者,由知,n(u,v)为常单位向量.因此d(x,n)=dx.n+x.dn=0+x.0=0,x.n=常值,即M为连通的平面(片).
相似问题
证明:曲面M:x(x y)=(x y f(x y))的第1 第2基本形式分别为证明:面积与曲面参数的
证明:曲面M:x(x,y)=(x,y,f(x,y))的第1、第2基本形式分别为证明:面积与曲面参数的选取无关(参阅定证明:面积与曲面参数的选取无关(参阅定理2.3.1
若平移曲面M:x(u v)=a(u)+b(v)的参数曲线构成正交网 证明:M必为柱面.请帮忙给出正确
若平移曲面M:x(u,v)=a(u)+b(v)的参数曲线构成正交网,证明:M必为柱面.请帮忙给出正确答案和分析,谢谢!
证明:挠曲线(τ(s)≠0)或非平面曲线(τ(s)≠0)的主法线曲面与从法线曲面都不是可展曲面.请帮
证明:挠曲线(τ(s)≠0)或非平面曲线(τ(s)≠0)的主法线曲面与从法线曲面都不是可展曲面.请帮忙给出正确答案和分析,谢谢!
举例说明R3中向量场X的奇点的指标可以为0.请帮忙给出正确答案和分析 谢谢!
举例说明R3中向量场X的奇点的指标可以为0.请帮忙给出正确答案和分析,谢谢!
证明:负常Gauss(总)曲率曲面设曲面的第1基本形式为I=v(du2+dv2) E=G=v F
证明:负常Gauss(总)曲率曲面设曲面的第1基本形式为I=v(du2+dv2), E=G=v, F=0.证明:测地线在uv设曲面的第1基本形式为I=v(du2+dv2), E=G=v, F=












