举例说明R3中向量场X的奇点的指标可以为0．请帮忙给出正确答案和分析 谢谢！
举例说明R3中向量场X的奇点的指标可以为0．
请帮忙给出正确答案和分析，谢谢！
参考解答
490***102
2024-11-16 23:52:08
正确答案：设M={(xy0)｜xy∈R)切向量场x=(x2+y200)显然它为C∞切向量场且(00)为其孤立奇点．但是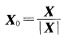
与X的方向始终指向x轴的正向所以φ≡0I=0．
设M={(x,y,0)｜x,y∈R),切向量场x=(x2+y2,0,0),显然它为C∞切向量场,且(0,0)为其孤立奇点．但是,与X的方向始终指向x轴的正向,所以φ≡0,I=0．
相似问题
证明：负常Gauss(总)曲率曲面设曲面的第1基本形式为I=v(du2＋dv2) E=G=v F
证明：负常Gauss(总)曲率曲面设曲面的第1基本形式为I=v(du2＋dv2)， E=G=v， F=0．证明：测地线在uv设曲面的第1基本形式为I=v(du2+dv2)， E=G=v， F=
设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn｜f(x)=0}≠∮ 且对C1曲面MC R
设f(x)为Rn上的一个Cr函数(r≥1)，M={x∈Rn｜f(x)=0}≠∮，且对C1曲面MC R3，它为可定向曲面M上存在一个C1曲面MC R3，它为可定向曲面M上存在一个连续的
设在曲面M上一点 含du dv的2次方程Pdu2+2Qdudv+Rdv2=0确定了两个切线方向．证明
设在曲面M上一点，含du，dv的2次方程Pdu2+2Qdudv+Rdv2=0确定了两个切线方向．证明：这两个方向相互正交ER一2FQ+GP=0．请帮忙给出正确答案和分析，谢谢！
设e1 e2 ω1 ω2和设R3中C2曲面M在等温参数{u v}下 第1基本形式：I=ds2=E(d
设e1，e2，ω1，ω2和设R3中C2曲面M在等温参数{u，v}下，第1基本形式：I=ds2=E(du2＋dv2)=λ2(du2＋dv2)，E=G设R3中C2曲面M在等温参数{u，v}下，第1基本
设圆柱螺线 设x(t)为C1参数曲线 m为固定向量．若对任何t x(t)正交于m 且x(0)正交于m
设圆柱螺线 设x(t)为C1参数曲线，m为固定向量．若对任何t，x(t)正交于m，且x(0)正交于m，证明：对任何设x(t)为C1参数曲线，m为固定向量．若对任何t，x(t
