设e1 e2 ω1 ω2和设R3中C2曲面M在等温参数{u v}下 第1基本形式:I=ds2=E(d
设e1,e2,ω1,ω2和设R3中C2曲面M在等温参数{u,v}下,第1基本形式:I=ds2=E(du2+dv2)=λ2(du2+dv2),E=G
设R3中C2曲面M在等温参数{u,v}下,第1基本形式:I=ds2=E(du2+dv2)=λ2(du2+dv2),E=G=λ2 (λ>0). (1)Laplace算子表达式为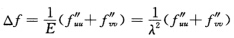 其中f为M上的C2函数; (2)Gauss曲率为
其中f为M上的C2函数; (2)Gauss曲率为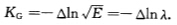
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)证法1取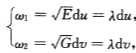 则
则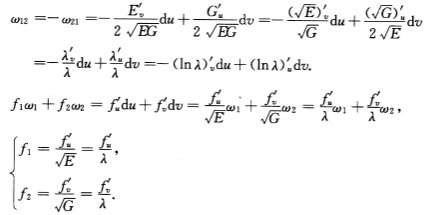 于是
于是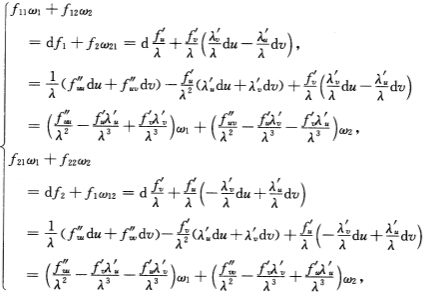
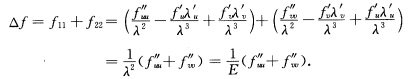 证法2根据习题3.2.3的证法2有
证法2根据习题3.2.3的证法2有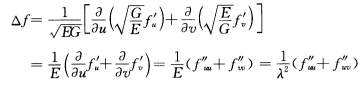 (2)证法1
(2)证法1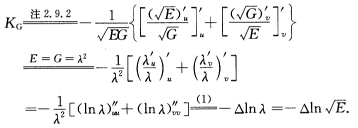 证法2根据[212.11节知
证法2根据[212.11节知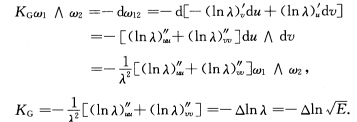
(1)证法1取则于是证法2根据习题3.2.3的证法2,有(2)证法1证法2根据[212.11节,知
相似问题
设圆柱螺线 设x(t)为C1参数曲线 m为固定向量.若对任何t x(t)正交于m 且x(0)正交于m
设圆柱螺线 设x(t)为C1参数曲线,m为固定向量.若对任何t,x(t)正交于m,且x(0)正交于m,证明:对任何设x(t)为C1参数曲线,m为固定向量.若对任何t,x(t
设平面2次连续可导的正则曲线的极坐标表示为x(θ)=r(θ)e(θ)=(r(θ)cosθ r(θ)s
设平面2次连续可导的正则曲线的极坐标表示为x(θ)=r(θ)e(θ)=(r(θ)cosθ,r(θ)sinθ),其中e(θ)=(cosθ,sinθ). 证明:该曲线的曲率在极坐标下的
证明:如果曲面M上k>0的测地线为平面曲线 则它必为曲率线.如果曲面M的所有测地线均为平面曲线且k>
证明:如果曲面M上k>0的测地线为平面曲线,则它必为曲率线.如果曲面M的所有测地线均为平面曲线且k>0,则曲面M为全脐曲面.进而,如果M连通,则M为球面片
求悬链线求曳物线x(t)=(acos t aln(sect+tant)-asin t 0)的弧长s
求悬链线求曳物线x(t)=(acos t,aln(sect+tant)-asin t,0)的弧长s,其中a>0,并用弧长为参数表示求曳物线x(t)=(acos t,aln(sect+tant)-asin t,0
设曲面M:x(u v)=(ucosv usinv lnu)与证明:曲面在点(u v)处Gauss(总
设曲面M:x(u,v)=(ucosv,usinv,lnu)与证明:曲面在点(u,v)处Gauss(总)曲率相等.但M与在此对应下未证明:曲面在点(u,v)处Gauss(总)曲率相等.但M与












