设平面2次连续可导的正则曲线的极坐标表示为x(θ)=r(θ)e(θ)=(r(θ)cosθ r(θ)s
设平面2次连续可导的正则曲线的极坐标表示为x(θ)=r(θ)e(θ)=(r(θ)cosθ，r(θ)sinθ)，其中e(θ)=(cosθ，sinθ)． 证明：该曲线的曲率在极坐标下的公式为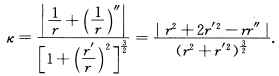
请帮忙给出正确答案和分析，谢谢！
参考解答
456***102
2024-11-16 23:37:42
正确答案：×
计算得e(θ)=(cosθ,sinθ),e'(θ)=(一sinθ,cosθ),e.e'=0,｜e×e'｜=1,e''(θ)=(一cosθ,一sinθ)=一e(θ)；X'=r'e+re',x''=r''e+2r'e'+re''=r''e+2r'e'一re=(r''一r)e+2r'e'。x'×x''=(r'e+re')×[(r''一r)e+2r'e'一e×e'[2r'2一r(r''一r)=e×e'(r'一rr''+2r'2)．于是从第2个等号可看出
相似问题
证明：如果曲面M上k>0的测地线为平面曲线 则它必为曲率线．如果曲面M的所有测地线均为平面曲线且k>
证明：如果曲面M上k>0的测地线为平面曲线，则它必为曲率线．如果曲面M的所有测地线均为平面曲线且k>0，则曲面M为全脐曲面．进而，如果M连通，则M为球面片
求悬链线求曳物线x(t)=(acos t aln(sect＋tant)－asin t 0)的弧长s
求悬链线求曳物线x(t)=(acos t，aln(sect＋tant)－asin t，0)的弧长s，其中a>0，并用弧长为参数表示求曳物线x(t)=(acos t，aln(sect+tant)-asin t，0
设曲面M：x(u v)=(ucosv usinv lnu)与证明：曲面在点(u v)处Gauss(总
设曲面M：x(u，v)=(ucosv，usinv，lnu)与证明：曲面在点(u，v)处Gauss(总)曲率相等．但M与在此对应下未证明：曲面在点(u，v)处Gauss(总)曲率相等．但M与
曲线C1:和C3:v=1所构成的三角形的边长与内角．1. 求下列曲面M的第1基本形式和第2基本形式I
曲线C1:和C3:v=1所构成的三角形的边长与内角．1 求下列曲面M的第1基本形式和第2基本形式I，Ⅱ： (1)椭球面：参数表示为X(Φ，Θ)=(ACOSΦCOSΘ，BCOS
证明：(1)平面上的点均为平点；(2)球面上的点均为圆点．请帮忙给出正确答案和分析 谢谢！
证明：(1)平面上的点均为平点；(2)球面上的点均为圆点．请帮忙给出正确答案和分析，谢谢！
