证明：(1)平面上的点均为平点；(2)球面上的点均为圆点．请帮忙给出正确答案和分析 谢谢！

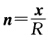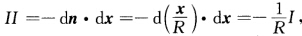正确答案：证法1 (1)在平面上n=const(常单位向量)故dn=0且Ⅱ=一dn.dx=0.dx=0=0.I所以平面上的点均为平点．(2)不妨考虑中心在原点、半径为R的球面单位法向量则由于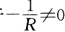所以球面上的点均为圆点．证法2 (1)不妨设平面为x(xy)=(xy0)．由例2．6．2或由x_xx^''=x_xy^''=x_yx^''=x_yy^''=0L=x_xx^''.n=0M=x_xy^''.n=0N=x_yy^''.n=0立知Ⅱ=Ldx²+2Mdxdy+Ndy²=0=0.I.所以平面上的点均为平点．(2)由例2．6．3或习题2．3．9或直接计算得x(uv)=(Rsin vcosuRsin vsinuRcosv)x_u^'(uv)=(一Rsin vsinuRsin vcosu0)x_v^'(uv)=(RcosvcosuRcos vsinu一Rsinv)E=x_u^'.x_u^'=R²sin²vF=x_u^'.x_v^'=0G=x_v^'.x_v^'=R²．于是单位法向量为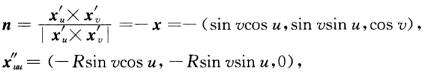x_uv^''=(一Rcos vsinuRcos vcosu0)x_vv^''=(一Rsinvcosu一Rsin vsinu一Rcosv)L=x_uu^''.n=Rsin²nM=x_uv^''.n=0N=x_vv^''n=R．于是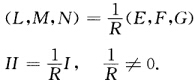这就证明了球面上的点均为圆点．
证法1(1)在平面上n=const(常单位向量),故dn=0,且Ⅱ=一dn.dx=0.dx=0=0.I,所以平面上的点均为平点．(2)不妨考虑中心在原点、半径为R的球面,单位法向量则由于所以球面上的点均为圆点．证法2(1)不妨设平面为x(x,y)=(x,y,0)．由例2．6．2,或由xxx''=xxy''=xyx''=xyy''=0,L=xxx''.n=0,M=xxy''.n=0,N=xyy''.n=0,立知Ⅱ=Ldx2+2Mdxdy+Ndy2=0=0.I.所以平面上的点均为平点．(2)由例2．6．3或习题2．3．9,或直接计算得x(u,v)=(Rsinvcosu,Rsinvsinu,Rcosv),xu'(u,v)=(一Rsinvsinu,Rsinvcosu,0),xv'(u,v)=(Rcosvcosu,Rcosvsinu,一Rsinv),E=xu'.xu'=R2sin2v,F=xu'.xv'=0,G=xv'.xv'=R2．于是,单位法向量为xuv''=(一Rcosvsinu,Rcosvcosu,0),xvv''=(一Rsinvcosu,一Rsinvsinu,一Rcosv),L=xuu''.n=Rsin2n,M=xuv''.n=0,N=xvv'',n=R．于是这就证明了球面上的点均为圆点．