R3中k≠0 τ≠0的C4连通曲线x(s)为球面曲线等价于设曲线C:x(s)(s为弧长)为常挠曲率曲
R3中k≠0,τ≠0的C4连通曲线x(s)为球面曲线等价于设曲线C:x(s)(s为弧长)为常挠曲率曲线.证明曲线:为
设曲线C:x(s)(s为弧长)为常挠曲率曲线.证明曲线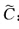 :
: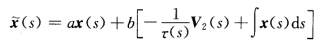 为x(s)的Bertrand侣线,其中a,b为常数,k,τ,V2分别为x(s)的曲率、挠率和主法向量,x(s)为其本身的从法向量,即x(s)=V3(s).
为x(s)的Bertrand侣线,其中a,b为常数,k,τ,V2分别为x(s)的曲率、挠率和主法向量,x(s)为其本身的从法向量,即x(s)=V3(s).
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:计算得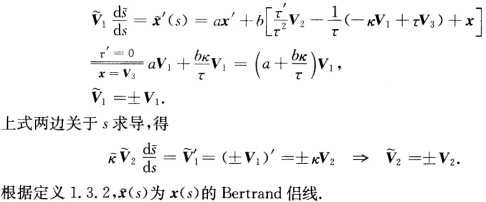
计算得
相似问题
设曲面M:x(u v)=(ucosv usinv lnu)与(ucosv usinv v)在对应(u
设曲面M:x(u,v)=(ucosv,usinv,lnu)与(ucosv,usinv,v)在对应(u,v)→(u,v)下,Gauss(总)曲率相等,但此对应不是等距映射.请帮忙给出正确答案和分析,谢谢!
求旋转曲面M:x(u v)=(f(u)cosv f(u)sinv u) (f(u)>0)的测地线.设
求旋转曲面M:x(u,v)=(f(u)cosv,f(u)sinv,u) (f(u)>0)的测地线.设θ为测地线与经线的交角,f为交点到旋转轴之间的距离.证明:f(u)sinθ=常数. (2
X=(x y);请帮忙给出正确答案和分析 谢谢!
X=(x,y);请帮忙给出正确答案和分析,谢谢!
证明:如果劈锥曲面x(u v)=(ucosv usinv φ(v))(φ(v)≠0)为极小曲面 则它
证明:如果劈锥曲面x(u,v)=(ucosv,usinv,φ(v))(φ(v)≠0)为极小曲面,则它必为正螺面.请帮忙给出正确答案和分析,谢谢!
设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn|f(x)=0}≠∮ 且对设M为R3中的一
设f(x)为Rn上的一个Cr函数(r≥1),M={x∈Rn|f(x)=0}≠∮,且对设M为R3中的一个2维Ck(k≥1)正则曲面,点P∈设M为R3中的一个2维Ck(k≥1)正则曲面,点P∈M












