参考解答
406***102
2024-11-16 23:07:04
正确答案：(00)为孤立奇点的验算是平凡的．单位圆C为环路以θ为参数0≤θ《2π．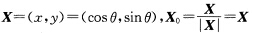
沿单位圆C按逆时针方向转动x0与e1的夹角φ从0变到2π(习题3．4．1图(I))故指标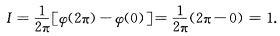
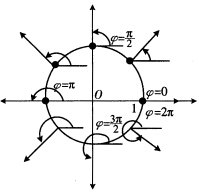
(0,0)为孤立奇点的验算是平凡的．单位圆C为环路,以θ为参数,0≤θ《2π．沿单位圆C按逆时针方向转动,x0与e1的夹角φ从0变到2π(习题3．4．1图(I)),故指标
相似问题
证明：如果劈锥曲面x(u v)=(ucosv usinv φ(v))(φ(v)≠0)为极小曲面 则它
证明：如果劈锥曲面x(u，v)=(ucosv，usinv，φ(v))(φ(v)≠0)为极小曲面，则它必为正螺面．请帮忙给出正确答案和分析，谢谢！
设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn｜f(x)=0}≠∮ 且对设M为R3中的一
设f(x)为Rn上的一个Cr函数(r≥1)，M={x∈Rn｜f(x)=0}≠∮，且对设M为R3中的一个2维Ck(k≥1)正则曲面，点P∈设M为R3中的一个2维Ck(k≥1)正则曲面，点P∈M
设P0为两曲线x(s)与的交点 在P0的一旁邻近取点P1 P2 它们分别属于曲线x(s)与 且使曲线
设P0为两曲线x(s)与的交点，在P0的一旁邻近取点P1，P2，它们分别属于曲线x(s)与，且使曲线弧长． 若 则称曲线x(s)与 在P0点有n阶接触． 证明： (1)
计算悬链面M：的第1 第2基本形式．请帮忙给出正确答案和分析 谢谢！
计算悬链面M：的第1、第2基本形式．请帮忙给出正确答案和分析，谢谢！
证明：负常Gauss(总)曲率曲面的第1基本形式可取为：．请帮忙给出正确答案和分析 谢谢！
证明：负常Gauss(总)曲率曲面的第1基本形式可取为：．请帮忙给出正确答案和分析，谢谢！
