设P0为两曲线x(s)与的交点 在P0的一旁邻近取点P1 P2 它们分别属于曲线x(s)与 且使曲线
设P0为两曲线x(s)与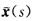 的交点,在P0的一旁邻近取点P1,P2,它们分别属于曲线x(s)与
的交点,在P0的一旁邻近取点P1,P2,它们分别属于曲线x(s)与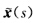 ,且使曲线弧长
,且使曲线弧长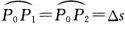 . 若
. 若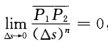 则称曲线x(s)与
则称曲线x(s)与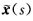 在P0点有n阶接触. 证明: (1)两曲线x(s)与
在P0点有n阶接触. 证明: (1)两曲线x(s)与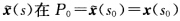 具有n阶接触等价于
具有n阶接触等价于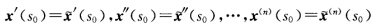 ; (2)曲线x(s)的切线y(s)=x(s0)+(s一s0)x(s0)与曲线x(s)在s0有1阶接触的唯一直线; (3)若连通C2曲线x(s)每一点的切线与曲线x(s)有2阶接触,则曲线x(s)为直线.
; (2)曲线x(s)的切线y(s)=x(s0)+(s一s0)x(s0)与曲线x(s)在s0有1阶接触的唯一直线; (3)若连通C2曲线x(s)每一点的切线与曲线x(s)有2阶接触,则曲线x(s)为直线.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:在s0点作Taylor展开: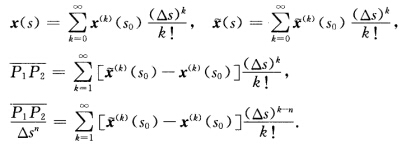 (1)
(1)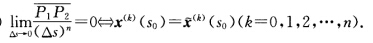 (2)由于y'(s)=[x(s0)+(s一s0)x'(s0)'=x'(s0)根据(1)切线y(s)与曲线x(s)在s0有1阶接触.又若直线Z(x)=x(s0)+(s一s0)a(a为常单位向量)与曲线x(s)在s0有1阶接触则a=Z'(s0)=x'(s0)Z(s)=x(s0)+(s—s0)s=x(s0)+(s—s0)x'(s0)它为曲线x(s)在s0的切线.因此切线y(s)是曲线x(s)在s0有1阶接触的唯一直线.(3)若切线y(s)=x(s0)+(s—s0)x'(s0)在任何s0与x(s)有2阶接触则x(s0)=y(s0)=0即x'(s)≡0.积分得x'(s)=x'(s0).再积分就有x(s)=x(s0)+(s—s0)x'(s0)即连通C2曲线x(s)为直线.
(2)由于y'(s)=[x(s0)+(s一s0)x'(s0)'=x'(s0)根据(1)切线y(s)与曲线x(s)在s0有1阶接触.又若直线Z(x)=x(s0)+(s一s0)a(a为常单位向量)与曲线x(s)在s0有1阶接触则a=Z'(s0)=x'(s0)Z(s)=x(s0)+(s—s0)s=x(s0)+(s—s0)x'(s0)它为曲线x(s)在s0的切线.因此切线y(s)是曲线x(s)在s0有1阶接触的唯一直线.(3)若切线y(s)=x(s0)+(s—s0)x'(s0)在任何s0与x(s)有2阶接触则x(s0)=y(s0)=0即x'(s)≡0.积分得x'(s)=x'(s0).再积分就有x(s)=x(s0)+(s—s0)x'(s0)即连通C2曲线x(s)为直线.
在s0点作Taylor展开:(1)(2)由于y'(s)=[x(s0)+(s一s0)x'(s0)'=x'(s0),根据(1),切线y(s)与曲线x(s)在s0有1阶接触.又若直线Z(x)=x(s0)+(s一s0)a(a为常单位向量)与曲线x(s)在s0有1阶接触,则a=Z'(s0)=x'(s0),Z(s)=x(s0)+(s—s0)s=x(s0)+(s—s0)x'(s0),它为曲线x(s)在s0的切线.因此,切线y(s)是曲线x(s)在s0有1阶接触的唯一直线.(3)若切线y(s)=x(s0)+(s—s0)x'(s0)在任何s0与x(s)有2阶接触,则x(s0)=y(s0)=0,即x'(s)≡0.积分得x'(s)=x'(s0).再积分,就有x(s)=x(s0)+(s—s0)x'(s0),即连通C2曲线x(s)为直线.
相似问题
计算悬链面M:的第1 第2基本形式.请帮忙给出正确答案和分析 谢谢!
计算悬链面M:的第1、第2基本形式.请帮忙给出正确答案和分析,谢谢!
证明:负常Gauss(总)曲率曲面的第1基本形式可取为:.请帮忙给出正确答案和分析 谢谢!
证明:负常Gauss(总)曲率曲面的第1基本形式可取为:.请帮忙给出正确答案和分析,谢谢!
设f(x)是[0 +∞)上的单调减少函数 证明:对任何满足λ+μ=1的正数λ μ及x∈[0 +∞)
设f(x)是[0,+∞)上的单调减少函数, 证明:对任何满足λ+μ=1的正数λ,μ及x∈[0,+∞)有下列不等式成立: f(x)≤λf(λx)+μf(μx); (2)设是(0,
举例说明R3中非紧致曲面M上的切向量场X可能有无限多个孤立奇点.请帮忙给出正确答案和分析 谢谢!
举例说明R3中非紧致曲面M上的切向量场X可能有无限多个孤立奇点.请帮忙给出正确答案和分析,谢谢!
两条C3曲线设κ(s)与τ(s)分别为曲线x(s)的曲率与挠率 其中s为其弧长 它的单位切向量可视作
两条C3曲线设κ(s)与τ(s)分别为曲线x(s)的曲率与挠率,其中s为其弧长,它的单位切向量可视作单位球设κ(s)与τ(s)分别为曲线x(s)的曲率与挠率,其中s为












