设f(x)是[0 +∞)上的单调减少函数 证明：对任何满足λ+μ＝1的正数λ μ及x∈[0 +∞)
设f(x)是[0，+∞)上的单调减少函数， 证明：对任何满足λ+μ＝1的正数λ，μ及x∈[0，+∞)有下列不等式成立： f(x)≤λf(λx)+μf(μx)； (2)设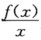
是(0，+∞)内的单调减少函数，证明：对任何满足λ+μ＝1的正数λ，μ及x∈(0，+∞)有下列不等式成立： f(x)≤f(λx)+f(μx)． 并由此证明：对任何正数a，b，有下列不等式成立： f(a+b)≤f(a)+f(b)．
请帮忙给出正确答案和分析，谢谢！
参考解答
413***102
2024-11-16 22:55:03
正确答案：证明 Vx∈[0+∞)λ+μ＝1．λ＝1f(x)在[0+∞上单调减少且x≥λxx≥μx则有 f(x)≤f(λx) ① f(f)≤f(μx) ② λ①+μ② λf(x)+μf(x)≤λf(λx)+μf(μx) (λ+μ)f(x)≤λf(λx)+μf(μz) f(x)≤λf(λx)+μf(μx)
证明Vx∈[0,+∞),λ+μ＝1．λ＝1f(x)在[0,+∞上单调减少,且x≥λx,x≥μx则有f(x)≤f(λx)①f(f)≤f(μx)②λ①+μ②λf(x)+μf(x)≤λf(λx)+μf(μx)(λ+μ)f(x)≤λf(λx)+μf(μz)f(x)≤λf(λx)+μf(μx)
相似问题
举例说明R3中非紧致曲面M上的切向量场X可能有无限多个孤立奇点．请帮忙给出正确答案和分析 谢谢！
举例说明R3中非紧致曲面M上的切向量场X可能有无限多个孤立奇点．请帮忙给出正确答案和分析，谢谢！
两条C3曲线设κ(s)与τ(s)分别为曲线x(s)的曲率与挠率 其中s为其弧长 它的单位切向量可视作
两条C3曲线设κ(s)与τ(s)分别为曲线x(s)的曲率与挠率，其中s为其弧长，它的单位切向量可视作单位球设κ(s)与τ(s)分别为曲线x(s)的曲率与挠率，其中s为
证明：曲面M：x(x y)=(x y f(x y))的第1 第2基本形式分别为请帮忙给出正确答案和分
证明：曲面M：x(x，y)=(x，y，f(x，y))的第1、第2基本形式分别为请帮忙给出正确答案和分析，谢谢！
两条C3曲线请帮忙给出正确答案和分析 谢谢！
两条C3曲线请帮忙给出正确答案和分析，谢谢！
求旋轮线(摆线)x(t)=(a(r一sint) a(1一cost))的相对曲率kr(弧长s增加的方向
求旋轮线(摆线)x(t)=(a(r一sint)，a(1一cost))的相对曲率kr(弧长s增加的方向就是参数增加的方向)．请帮忙给出正确答案和分析，谢谢！
