设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn｜f(x)=0}≠∮ 且对C1曲面MC R

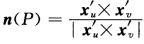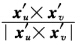正确答案：(→)设M为可定向曲面则可用一族坐标邻域覆盖M使得在任意两个坐标邻域的交集中坐标转换函数有正的Jacobi行列式．因此在每个坐标邻域U中若P∈UP=x(uv)则定义单位法向量易见n(P)与P所在的定向坐标系的选取无关则n(P)为M上的连续单位法向量场．(←)设M上存在一个连续的单位法向量场n(P)．考虑一族覆盖M的连通的坐标系{(U_aφ_a)｜a∈F．设(U_aφ_a)的局部坐标为{uv．由于也是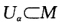上的连续单位法向量场因此对P∈U_a必有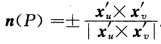但是由于U_a连通故在U_a上上述等式必须恒取“+”号或恒取“一”号．于是在U_a上我们可选局部坐标{uv使得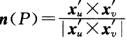(若取“一”号只需交换uv的次序或换为u一v得到新坐标使得上式成立)．在每个U_a中都采用上述方法选取局部坐标系．此时在任意两个这样的局部坐标邻域的交集中坐标转换的Jacobi行列式为正的从而M为可定向曲面．
(→)设M为可定向曲面,则可用一族坐标邻域覆盖M,使得在任意两个坐标邻域的交集中,坐标转换函数有正的Jacobi行列式．因此,在每个坐标邻域U中,若P∈U,P=x(u,v),则定义单位法向量易见,n(P)与P所在的定向坐标系的选取无关则n(P)为M上的连续单位法向量场．(←)设M上存在一个连续的单位法向量场n(P)．考虑一族覆盖M的连通的坐标系{(Ua,φa)｜a∈F．设(Ua,φa)的局部坐标为{u,v．由于也是上的连续单位法向量场,因此,对P∈Ua,必有但是,由于Ua连通,故在Ua上,上述等式必须恒取“+”号或恒取“一”号．于是,在Ua上我们可选局部坐标{u,v,使得(若取“一”号,只需交换u,v的次序或换为u,一v得到新坐标,使得上式成立)．在每个Ua中都采用上述方法选取局部坐标系．此时,在任意两个这样的局部坐标邻域的交集中,坐标转换的Jacobi行列式为正的,从而M为可定向曲面．