证明:负常Gauss(总)曲率曲面设曲面的第1基本形式为I=v(du2+dv2) E=G=v F
证明:负常Gauss(总)曲率曲面设曲面的第1基本形式为I=v(du2+dv2), E=G=v, F=0.证明:测地线在uv
设曲面的第1基本形式为I=v(du2+dv2), E=G=v, F=0.证明:测地线在uv平面上为一条抛物线.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由测地线的微分方程得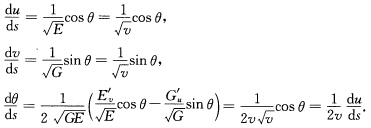 由前两个方程得
由前两个方程得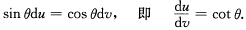 由最后一个方程得
由最后一个方程得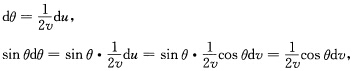 则有
则有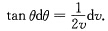 两边积分得
两边积分得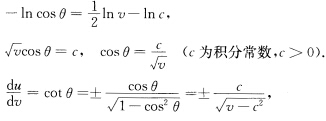 所以
所以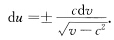 再积分得
再积分得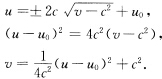 因此所求的测地线在uv平面上是抛物线(参阅习题2.8.8(2)).
因此所求的测地线在uv平面上是抛物线(参阅习题2.8.8(2)).
由测地线的微分方程得由前两个方程得由最后一个方程得则有两边积分得所以再积分得因此,所求的测地线在uv平面上是抛物线(参阅习题2.8.8(2)).
相似问题
设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn|f(x)=0}≠∮ 且对C1曲面MC R
设f(x)为Rn上的一个Cr函数(r≥1),M={x∈Rn|f(x)=0}≠∮,且对C1曲面MC R3,它为可定向曲面M上存在一个C1曲面MC R3,它为可定向曲面M上存在一个连续的
设在曲面M上一点 含du dv的2次方程Pdu2+2Qdudv+Rdv2=0确定了两个切线方向.证明
设在曲面M上一点,含du,dv的2次方程Pdu2+2Qdudv+Rdv2=0确定了两个切线方向.证明:这两个方向相互正交ER一2FQ+GP=0.请帮忙给出正确答案和分析,谢谢!
设e1 e2 ω1 ω2和设R3中C2曲面M在等温参数{u v}下 第1基本形式:I=ds2=E(d
设e1,e2,ω1,ω2和设R3中C2曲面M在等温参数{u,v}下,第1基本形式:I=ds2=E(du2+dv2)=λ2(du2+dv2),E=G设R3中C2曲面M在等温参数{u,v}下,第1基本
设圆柱螺线 设x(t)为C1参数曲线 m为固定向量.若对任何t x(t)正交于m 且x(0)正交于m
设圆柱螺线 设x(t)为C1参数曲线,m为固定向量.若对任何t,x(t)正交于m,且x(0)正交于m,证明:对任何设x(t)为C1参数曲线,m为固定向量.若对任何t,x(t
设平面2次连续可导的正则曲线的极坐标表示为x(θ)=r(θ)e(θ)=(r(θ)cosθ r(θ)s
设平面2次连续可导的正则曲线的极坐标表示为x(θ)=r(θ)e(θ)=(r(θ)cosθ,r(θ)sinθ),其中e(θ)=(cosθ,sinθ). 证明:该曲线的曲率在极坐标下的












