证明：(1)证明：正螺面M：x(u v)=(vcosu vsinu bu) (0≤u≤2π 一∞

正确答案：证法1 (参阅例1．2．3、例2．7．8与习题2．7．7)正螺面上圆柱螺线的主法线为直母线．正螺面为圆柱螺线的主法线曲面．从而圆柱螺线的密切平面重合于正螺面的切平面．根据定理2．4．5圆柱螺线为渐近曲线．再根据定理2．4．4正螺面上的直线必为渐近线故直母线为渐近线．证法2从定义2．4．3知渐近曲线满足微分方程：Ldu²+2Mdudv+Ndv²=0．再从例2．7．8得到正螺面的第2基本形式的系数为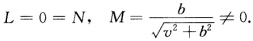因此上述渐近曲线的微分方程就成为Mdudv=0 即 dudv=0．由此推得坐标线必满足dudv=0故它们为渐近曲线．从而正螺面的直母线与圆柱螺线必为渐近曲线．注但是习题2．4．7中满足dudv=0的光滑曲线未必只有u=常数或v=常数．如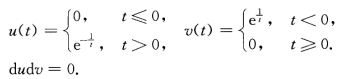：如果x(uv)为光滑正则曲面(u(t)v(t))为参数平面上的光滑曲线t∈(ab)则x(u(t)u(t))为该曲面上的光滑正则曲线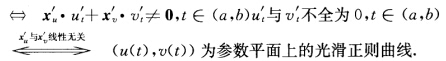由此当t∈(ab)且dudv=0时U₁={t∈(ab)｜u_t^'≠0 U₂={t∈(ab)｜v_t^'≠0为(ab)中不相交的开集且(ab)=U₁UU₂从(ab)连通立知U₁=∮U₂=(ab)此时u_t^'≡0u=常数(v曲线)；或者U₂=∮U₁=(ab)此时v_t^'≡0v_t^'=常数(u曲线)．因此正螺面上正则光滑曲线x(u(t)v(t))为渐近曲线它必为参数曲线即直母线与圆柱螺线．
证法1(参阅例1．2．3、例2．7．8与习题2．7．7)正螺面上圆柱螺线的主法线为直母线．正螺面为圆柱螺线的主法线曲面．从而,圆柱螺线的密切平面重合于正螺面的切平面．根据定理2．4．5,圆柱螺线为渐近曲线．再根据定理2．4．4,正螺面上的直线必为渐近线,故直母线为渐近线．证法2从定义2．4．3知,渐近曲线满足微分方程：Ldu2+2Mdudv+Ndv2=0．再从例2．7．8得到正螺面的第2基本形式的系数为因此,上述渐近曲线的微分方程就成为Mdudv=0,即dudv=0．由此推得坐标线必满足dudv=0,故它们为渐近曲线．从而,正螺面的直母线与圆柱螺线必为渐近曲线．注但是,习题2．4．7中满足dudv=0的光滑曲线未必只有u=常数或v=常数．如：如果x(u,v)为光滑正则曲面,(u(t),v(t))为参数平面上的光滑曲线,t∈(a,b),则x(u(t),u(t))为该曲面上的光滑正则曲线由此,当t∈(a,b),且dudv=0时,U1={t∈(a,b)｜ut'≠0,U2={t∈(a,b)｜vt'≠0为(a,b)中不相交的开集,且(a,b)=U1UU2从(a,b)连通立知U1=∮,U2=(a,b),此时ut'≡0,u=常数(v曲线)；或者U2=∮,U1=(a,b),此时vt'≡0,vt'=常数(u曲线)．因此,正螺面上正则光滑曲线x(u(t),v(t))为渐近曲线,它必为参数曲线,即直母线与圆柱螺线．