已知一组数据：(－3 9) (－2 6) (0 2) (1 1) 求数据拟合的最佳二次抛物线 并计算
已知一组数据：(－3，9)，(－2，6)，(0，2)，(1，1)，求数据拟合的最佳二次抛物线，并计算误差．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***101
2024-11-11 22:17:53
正确答案：本题实际上是要求参数βi使函数y=β0+β1+β2xi最佳拟合数据点(－39) (－26)(02)(11)．也即求方程组
的最佳逼近解．因系数矩阵A是列满秩的求得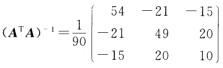
故最佳逼近解为
于是数据拟合的最佳二次抛物线为
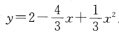．误差为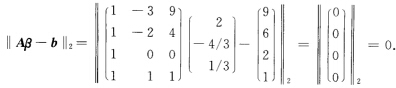
本题实际上是要求参数βi,使函数y=β0+β1+β2xi最佳拟合数据点(－3,9),(－2,6),(0,2),(1,1)．也即求方程组的最佳逼近解．因系数矩阵A是列满秩的,求得,故最佳逼近解为于是数据拟合的最佳二次抛物线为．误差为
相似问题
设A∈Rm×n C∈Rn×n都是可逆矩阵 证明：若矩阵B∈Rm×n是左(右)可逆的 则矩阵ABC也是
设A∈Rm×n，C∈Rn×n都是可逆矩阵，证明：若矩阵B∈Rm×n是左(右)可逆的，则矩阵ABC也是左(右)可逆的．请帮忙给出正确答案和分析，谢谢！
举例说明： (1)在由两个盖尔圆构成的连通部分中 可以在每一个盖尔圆中恰有一个特征值． (2)不一定
举例说明： (1)在由两个盖尔圆构成的连通部分中，可以在每一个盖尔圆中恰有一个特征值． (2)不一定每个盖尔圆中必有一个特征值．请帮忙给出正确答案和
设有可逆矩阵S∈Rn×n x∈Rn 且∥x∥s=∥Sx∥2是Rn上的向量范数． (1)若∥A∥s表示
设有可逆矩阵S∈Rn×n，x∈Rn，且∥x∥s=∥Sx∥2是Rn上的向量范数． (1)若∥A∥s表示Rn×n上从属于向量范数∥x∥s的算子范数，试导出∥A∥s与矩阵的2－
设α1 α2 … αn均为正数 X∈Cn 且x=(x1 x2 … xn)T．证明函数在Cn上定义了一
设α1，α2，…，αn均为正数，X∈Cn，且x=(x1，x2，…，xn)T．证明函数在Cn上定义了一个向量范数．请帮忙给出正确答案和分析，谢谢！
若A=(αij)是n阶正定矩阵 则有det(A)≤α11α22…αnn 当且仅当A为对角矩阵时等式才
若A=(αij)是n阶正定矩阵，则有det(A)≤α11α22…αnn，当且仅当A为对角矩阵时等式才成立(这就是Hadamard不等式)．请帮忙给出正确答案和分析，谢谢！
