举例说明: (1)在由两个盖尔圆构成的连通部分中 可以在每一个盖尔圆中恰有一个特征值. (2)不一定
举例说明: (1)在由两个盖尔圆构成的连通部分中,可以在每一个盖尔圆中恰有一个特征值. (2)不一定每个盖尔圆中必有一个特征值.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)如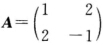 故∣λE-A∣=λ2-5=0
故∣λE-A∣=λ2-5=0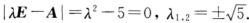 . (2)如
. (2)如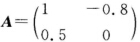 故∣λE-A∣=λ2-λ+0.4=0
故∣λE-A∣=λ2-λ+0.4=0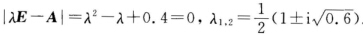
(1)如,故∣λE-A∣=λ2-5=0,.(2)如,故∣λE-A∣=λ2-λ+0.4=0,
相似问题
设有可逆矩阵S∈Rn×n x∈Rn 且∥x∥s=∥Sx∥2是Rn上的向量范数. (1)若∥A∥s表示
设有可逆矩阵S∈Rn×n,x∈Rn,且∥x∥s=∥Sx∥2是Rn上的向量范数. (1)若∥A∥s表示Rn×n上从属于向量范数∥x∥s的算子范数,试导出∥A∥s与矩阵的2-
设α1 α2 … αn均为正数 X∈Cn 且x=(x1 x2 … xn)T.证明函数在Cn上定义了一
设α1,α2,…,αn均为正数,X∈Cn,且x=(x1,x2,…,xn)T.证明函数在Cn上定义了一个向量范数.请帮忙给出正确答案和分析,谢谢!
若A=(αij)是n阶正定矩阵 则有det(A)≤α11α22…αnn 当且仅当A为对角矩阵时等式才
若A=(αij)是n阶正定矩阵,则有det(A)≤α11α22…αnn,当且仅当A为对角矩阵时等式才成立(这就是Hadamard不等式).请帮忙给出正确答案和分析,谢谢!
若A2=A 求sinA. (2)若A2=E 求sinA.请帮忙给出正确答案和分析 谢谢!
若A2=A,求sinA. (2)若A2=E,求sinA.请帮忙给出正确答案和分析,谢谢!
Α是n阶实矩阵 证明存在正交矩阵T 使T-1ΑT是三角矩阵的充要条件为Α的特征方程的根全是实数.请帮
Α是n阶实矩阵,证明存在正交矩阵T,使T-1ΑT是三角矩阵的充要条件为Α的特征方程的根全是实数.请帮忙给出正确答案和分析,谢谢!












