若A2=A 求sinA． (2)若A2=E 求sinA．请帮忙给出正确答案和分析 谢谢！
若A2=A，求sinA． (2)若A2=E，求sinA．
请帮忙给出正确答案和分析，谢谢！
参考解答
463***101
2024-11-11 21:50:57
正确答案：(1)若A2=A设rank(A)=γ则A的特征值为1或0于是必存在可逆矩阵P使得A可对角化为
故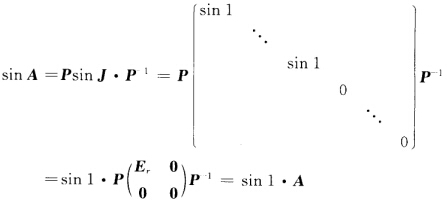
(2)当A2=E时A的特征值为1或－1设A有γ个特征值为1n－γ个特征值为－1则存在可逆矩阵P使得
于是
(1)若A2=A,设rank(A)=γ,则A的特征值为1或0,于是必存在可逆矩阵P,使得A可对角化为,故(2)当A2=E时,A的特征值为1或－1,设A有γ个特征值为1,n－γ个特征值为－1,则存在可逆矩阵P,使得,于是
相似问题
Α是n阶实矩阵 证明存在正交矩阵T 使T－1ΑT是三角矩阵的充要条件为Α的特征方程的根全是实数．请帮
Α是n阶实矩阵，证明存在正交矩阵T，使T－1ΑT是三角矩阵的充要条件为Α的特征方程的根全是实数．请帮忙给出正确答案和分析，谢谢！
设A∈Cm×n 证明(A－)T∈AT{1}．请帮忙给出正确答案和分析 谢谢！
设A∈Cm×n，证明(A－)T∈AT{1}．请帮忙给出正确答案和分析，谢谢！
试隔离矩阵A=的特征值．请帮忙给出正确答案和分析 谢谢！
试隔离矩阵A=的特征值．请帮忙给出正确答案和分析，谢谢！
设A B∈Cn×n均为正定的Hermite矩阵 则AB为正定的Hermite矩阵的充要条件是AB=B
设A，B∈Cn×n均为正定的Hermite矩阵，则AB为正定的Hermite矩阵的充要条件是AB=BA．请帮忙给出正确答案和分析，谢谢！
应用Ostrowski定理(或推论) 证明的谱半径γ(A)小于13．请帮忙给出正确答案和分析 谢谢！
应用Ostrowski定理(或推论)，证明的谱半径γ(A)小于13．请帮忙给出正确答案和分析，谢谢！
