设函数f(x)在闭区间[a b]上连续 在开区间(a b)内可导 且f(x)＞0．若极限存在 证明：

正确答案：[详解1(1)因为f(x)在[ab上连续且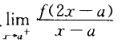存在故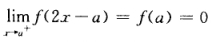又f'(x)＞0于是f(x)在(ab)内单调增加故 f(x)＞f(a)＝0x∈(ab)． (2)设F(x)＝x²g(x)＝∫_a^xf(t)dt(a≤x≤b)则g'(x)＝f(x)＞0故F(x)g(x)满足柯西中值定理的条件于是在(ab)内存在点ξ使 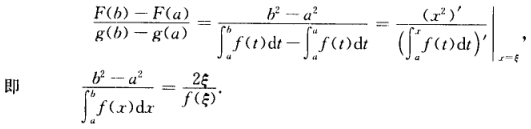(3)因f(ξ)＝f(ξ)－f(0)＝f(ξ)－(a)在[a
[分析(1)由存在知，f(a)＝0，利用单调性即可证明f(x)＞0．(2)要证的结论显含f(a)，f(b)，应将要证的结论写为拉格朗日中值定理或柯西中值定理的形式进行证明．(3)注意利用(2)的结论证明即可．此题也可用罗尔定理证明．[评注证明(3)，关键是用(2)的结论：可见对f(T)在区间[a，ξ上应用拉格朗日中值定理即可．对于这类题目，应注意充分利用前面设的台阶，中值定理是高等数学的重点，而构造辅助函数又是解与中值定理有关的证明题的非常有用的方法之一，考生应逐步掌握这种方法，并在证明过程中注意推理的逻辑性和严密性．