设xOy平面上有正方形D＝{(x y)｜0≤x≤1 0≤y≤1)及直线l： x＋y＝t(t≥0)．若

大学本科已帮助：人时间:2024-11-09 17:37:31

设xOy平面上有正方形D＝{(x，y)｜0≤x≤1，0≤y≤1)及直线l： x＋y＝t(t≥0)．若S(t)表示正方形D位于直线l左下方部分的面积，试求∫0xS(t)dt(x≥0)。
请帮忙给出正确答案和分析，谢谢！

456***101

2024-11-09 17:37:31



正确答案：根据题设有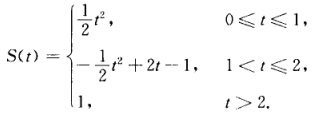可见当0≤x≤1时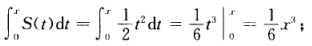当1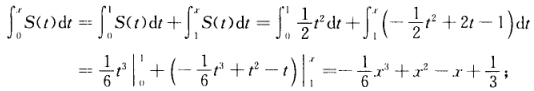＜x≤2时当x＞2时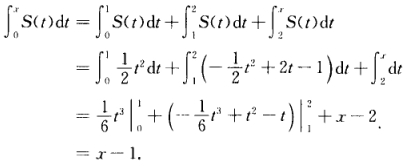故有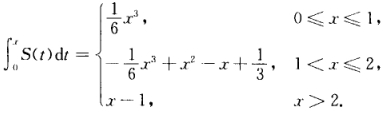
[分析首先根据，的不同取值，求出S(t)的表达式，然后再根据x的取值情况计算定积分∫0xS(t)dt(x≥0)．[评注分段函数的积分问题，应根据不同区间段上的函数表达式，利用积分的可加性分段进行积分。

[904*](x3＋sin2x)cos2xdx＝_______．请帮忙给出正确答案和分析谢谢！

[904*](x3＋sin2x)cos2xdx＝_______．请帮忙给出正确答案和分析，谢谢！
如图1－3－2 曲线C的方程为y＝f(x) 点(3 2)是它的一个拐点直线l1与l2分别是曲线C在

如图1－3－2，曲线C的方程为y＝f(x)，点(3，2)是它的一个拐点，直线l1与l2分别是曲线C在点(0，0)与(3，2)处的切线，其交点为(2，4)．设函数f(x)具有三阶
设函数f(x)连续且f(0)≠0 求极限。请帮忙给出正确答案和分析谢谢！

设函数f(x)连续，且f(0)≠0，求极限。请帮忙给出正确答案和分析，谢谢！
比较∫01｜ln t｜[ln(1＋t)]ndt与∫01t2｜ln t｜dt(n＝1 2 …)的大小

比较∫01｜ln t｜[ln(1＋t)]ndt与∫01t2｜ln t｜dt(n＝1，2，…)的大小，说明理由； (2)记un＝∫01｜ln t｜[ln(1＋t)ndt(n＝1，2，…)，求极限．请帮
设函数f(x)连续则下列函数中必为偶函数的是A．∫0xf(t2)dt．B．∫0xf2(t)dt．

设函数f(x)连续，则下列函数中，必为偶函数的是A．∫0xf(t2)dt．B．∫0xf2(t)dt．C．∫0xt[f(t)－f(－t)]dt．D．∫0xt[－f(t)＋f(－t)]dt．请帮忙给出正确答案和分析，谢谢！

[904*](x3＋sin2x)cos2xdx＝_______．请帮忙给出正确答案和分析谢谢！