设f(x) g(x)在[a b]上连续 且g(x)>0.利用闭区间上连续函数的性质 证明:存在一点ξ
设f(x),g(x)在[a,b]上连续,且g(x)>0.利用闭区间上连续函数的性质,证明:存在一点ξ∈[a,b],使∫abf(x)g(x)=f(ξ)∫abg(x)dx.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:利用f(x)g(x)在[ab上连续证明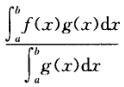 在f(x)的最大值与最小值之间再由介值定理即得.
在f(x)的最大值与最小值之间再由介值定理即得.
利用f(x),g(x)在[a,b上连续,证明在f(x)的最大值与最小值之间,再由介值定理即得.
相似问题
设函数f(x)在闭区间[a b]上连续 在开区间(a b)内可导 且f(x)>0.若极限存在 证明:
设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(x)>0.若极限存在,证明: (1)在(a,b)内f(x)>0; (2)在(a,b)内存在点ξ,使; (3)在
设D1是由抛物线y=2x2和直线x=a x=2及y=0所围成的平面区域;D2是由抛物线y=2x2和直
设D1是由抛物线y=2x2和直线x=a,x=2及y=0所围成的平面区域;D2是由抛物线y=2x2和直线y=0,x=a所围成的平面区域,其中0<a<2. (1)试求D1绕x轴旋
设xOy平面上有正方形D={(x y)|0≤x≤1 0≤y≤1)及直线l: x+y=t(t≥0).若
设xOy平面上有正方形D={(x,y)|0≤x≤1,0≤y≤1)及直线l: x+y=t(t≥0).若S(t)表示正方形D位于直线l左下方部分的面积,试求∫0xS(t)dt(x≥0)。请
[904*](x3+sin2x)cos2xdx=_______.请帮忙给出正确答案和分析 谢谢!
[904*](x3+sin2x)cos2xdx=_______.请帮忙给出正确答案和分析,谢谢!
如图1-3-2 曲线C的方程为y=f(x) 点(3 2)是它的一个拐点 直线l1与l2分别是曲线C在
如图1-3-2,曲线C的方程为y=f(x),点(3,2)是它的一个拐点,直线l1与l2分别是曲线C在点(0,0)与(3,2)处的切线,其交点为(2,4).设函数f(x)具有三阶












