设f(x1 x2 … xn)=XTAX是一实二次型 λ1 λ2 … λn是A的特征值 且λ1≤λ2≤
设f(x1，x2，…，xn)=XTAX是一实二次型，λ1，λ2，…，λn是A的特征值，且λ1≤λ2≤…≤λn证明：对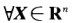
，有λ1XλTX≤XTAX≤nXTX．
请帮忙给出正确答案和分析，谢谢！
参考解答
473***101
2024-11-12 03:51:58
正确答案：由题意知A是实对称矩阵故存在正交矩阵Q使得Q－1AQ=diag(λ1λ2…λn)．其中λ1≤λ2≤…≤λn为A的n个特征值． 于是Q－1AQ－λ1E的特征值非负即矩阵A－λ1E半正定．于是对任意的实向量X有XT(A－λ1E)X≥0．故XTAX≥λ1XTX．同理可证XTAX≤λnXTX．所以λ1XTX≤XTAX≤λnXT
由题意知A是实对称矩阵,故存在正交矩阵Q,使得Q－1AQ=diag(λ1,λ2,…,λn)．其中λ1≤λ2≤…≤λn为A的n个特征值．于是Q－1AQ－λ1E的特征值非负,即矩阵A－λ1E半正定．于是对任意的实向量X,有XT(A－λ1E)X≥0．故XTAX≥λ1XTX．同理可证XTAX≤λnXTX．所以λ1XTX≤XTAX≤λnXT
相似问题
设A是n阶实对称矩阵．证明：A正定的充要条件是A的特征值全大于零．请帮忙给出正确答案和分析 谢谢！
设A是n阶实对称矩阵．证明：A正定的充要条件是A的特征值全大于零．请帮忙给出正确答案和分析，谢谢！
某大学数学测验 抽得20个学生的分数平均数机器包装食盐 假设每袋盐的净重服从正态分布 规定每袋机器包
某大学数学测验，抽得20个学生的分数平均数机器包装食盐，假设每袋盐的净重服从正态分布，规定每袋机器包装食盐，假设每袋盐的净重服从正态分布，规定每
求方程x2+y2=z2的整数解．请帮忙给出正确答案和分析 谢谢！
求方程x2+y2=z2的整数解．请帮忙给出正确答案和分析，谢谢！
设总体X的数学期望为μ X1 X2 … Xn是来自X的样本 a1 a2 … an是任意常数 验证一批
设总体X的数学期望为μ，X1，X2，…，Xn是来自X的样本，a1，a2，…，an是任意常数，验证一批发商产品中含有废一批发商产品中含有废品，从中随机地抽取60
设η是欧氏空间中一单位向量 定义T(α)=α－2(η α)η．证明： (1)T是正交变换 这样的正交
设η是欧氏空间中一单位向量，定义T(α)=α－2(η，α)η．证明： (1)T是正交变换，这样的正交变换称为镜面反射； (2)T是第二类的(即T对应的矩阵的行列
