参考解答
481***101
2024-11-12 03:42:50
正确答案：将不定方程写成矩阵行列式的形式由行列式为零知矩阵方程有非零解．再由此解出不定方程的整数解．首先将该方程写成行列式形式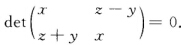
由行列式为零知以上述矩阵为系数的矩阵方程有非零解．故有不全为零的数a和b使得
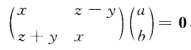即
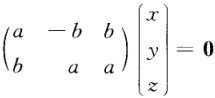解得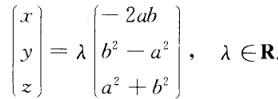
于是不定方程的整数解为
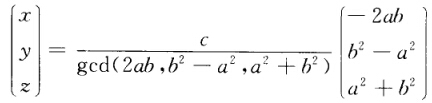其中ab和c为任意整数且a和b不全为零． 注 此题的更进一步形式即为1637年法国数学家费马(Fermat)提出的费马大定理：当自然数n>2时不定方程xn+yn=zn无正整数解．
将不定方程写成矩阵行列式的形式,由行列式为零知矩阵方程有非零解．再由此解出不定方程的整数解．首先,将该方程写成行列式形式由行列式为零,知以上述矩阵为系数的矩阵方程有非零解．故有不全为零的数a和b,使得即解得于是,不定方程的整数解为其中a,b和c为任意整数,且a和b不全为零．注此题的更进一步形式即为1637年法国数学家费马(Fermat)提出的费马大定理：当自然数n>2时,不定方程xn+yn=zn无正整数解．
相似问题
设总体X的数学期望为μ X1 X2 … Xn是来自X的样本 a1 a2 … an是任意常数 验证一批
设总体X的数学期望为μ，X1，X2，…，Xn是来自X的样本，a1，a2，…，an是任意常数，验证一批发商产品中含有废一批发商产品中含有废品，从中随机地抽取60
设η是欧氏空间中一单位向量 定义T(α)=α－2(η α)η．证明： (1)T是正交变换 这样的正交
设η是欧氏空间中一单位向量，定义T(α)=α－2(η，α)η．证明： (1)T是正交变换，这样的正交变换称为镜面反射； (2)T是第二类的(即T对应的矩阵的行列
某加油站替公共汽车站代营出租汽车业务 每出租一辆汽车 可以出租公司得到3元．因代营业务 每天加油站要
某加油站替公共汽车站代营出租汽车业务，每出租一辆汽车，可以出租公司得到3元．因代营业务，每天加油站要多付给队职工服务费60元，设每天出租汽车数X是
设T是线性空间V上的线性变换 证明：T对应的矩阵的行列式为零的充要条件是T以零作为一个特征值．请帮忙
设T是线性空间V上的线性变换，证明：T对应的矩阵的行列式为零的充要条件是T以零作为一个特征值．请帮忙给出正确答案和分析，谢谢！
某大学数学测验 抽得20个学生的分数平均数随机地取某种炮弹9发做试验 得炮口速度的样本标准差s=1随
某大学数学测验，抽得20个学生的分数平均数随机地取某种炮弹9发做试验，得炮口速度的样本标准差s=1随机地取某种炮弹9发做试验，得炮口速度的样本标准差s=
