应用Gauss—Bonnet公式证明：如果曲面M上存在两族交于定角θ的测地线 则M的Gauss(总)
应用Gauss—Bonnet公式证明：如果曲面M上存在两族交于定角θ的测地线，则M的Gauss(总)曲率处处为零．
请帮忙给出正确答案和分析，谢谢！
参考解答
473***102
2024-11-16 21:46:26
正确答案：(反证)假设存在点P0∈M使得KG(P0)≠0不妨设KG(P0)>0．由于KG(P)为P的连续函数故必有P0的开邻域U使KG(P)在U上与KG(P0)同号．再在U中取4条测地线组成四边形相对的两条属于题中所指的同一族两族交于定角θ并围成单连通区域D(见习题3．3．6图)．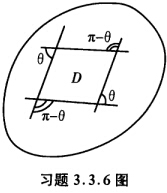
因此根据Gauss—B0nnet公式有
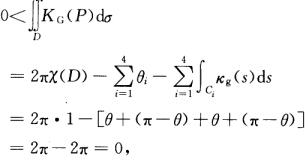矛盾．
(反证)假设存在点P0∈M,使得KG(P0)≠0,不妨设KG(P0)>0．由于KG(P)为P的连续函数,故必有P0的开邻域U,使KG(P)在U上与KG(P0)同号．再在U中取4条测地线组成四边形,相对的两条属于题中所指的同一族,两族交于定角θ,并围成单连通区域D(见习题3．3．6图)．因此,根据Gauss—B0nnet公式,有矛盾．
相似问题
设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn｜f(x)=0}≠∮ 且对证明：R3中环面
设f(x)为Rn上的一个Cr函数(r≥1)，M={x∈Rn｜f(x)=0}≠∮，且对证明：R3中环面T2是可定向的．证明：R3中环面T2是可定向的．请帮忙给出正确答案和分析，谢谢！
求悬链面M：上的渐近曲线．请帮忙给出正确答案和分析 谢谢！
求悬链面M：上的渐近曲线．请帮忙给出正确答案和分析，谢谢！
证明：Mbbius带是不可定向的．请帮忙给出正确答案和分析 谢谢！
证明：Mbbius带是不可定向的．请帮忙给出正确答案和分析，谢谢！
对于R3中2维定向光滑闭曲面(紧致 无边的曲面称为闭曲面)M Gauss映射G：M→S2为满射．请帮
对于R3中2维定向光滑闭曲面(紧致、无边的曲面称为闭曲面)M，Gauss映射G：M→S2为满射．请帮忙给出正确答案和分析，谢谢！
两条C3曲线与x(s)之间建立了一一对应关系 使它们在对应点的切线平行． 证明：它们在对应点的主法线
两条C3曲线与x(s)之间建立了一一对应关系，使它们在对应点的切线平行． 证明：它们在对应点的主法线以及从法线也分别平行，而且它们的曲率与挠率也都成
