两条C3曲线与x(s)之间建立了一一对应关系 使它们在对应点的切线平行. 证明:它们在对应点的主法线
两条C3曲线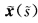 与x(s)之间建立了一一对应关系,使它们在对应点的切线平行. 证明:它们在对应点的主法线以及从法线也分别平行,而且它们的曲率与挠率也都成比例,其中
与x(s)之间建立了一一对应关系,使它们在对应点的切线平行. 证明:它们在对应点的主法线以及从法线也分别平行,而且它们的曲率与挠率也都成比例,其中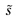 与s分别为
与s分别为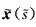 与x(s)的弧长.因此,如果x(s)为一般螺线,则
与x(s)的弧长.因此,如果x(s)为一般螺线,则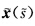 也为一般螺线.
也为一般螺线.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:因为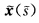 与x(s)在对应点的切线平行故
与x(s)在对应点的切线平行故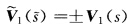 .根据Frenet公式有
.根据Frenet公式有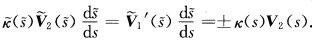 由于
由于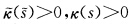 所以
所以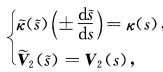 从而有
从而有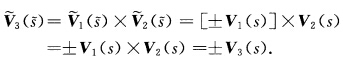 再根据Frenet公式有
再根据Frenet公式有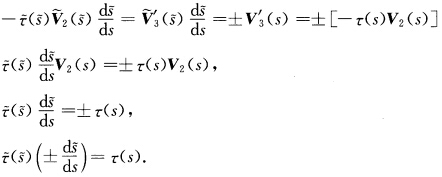 综合上述得到
综合上述得到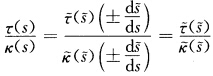 这就证明了它们在对应点的主法线以及从法线也分别平行而且它们的曲率与挠率也都成正比例.如果x(s)为一般螺线根据例1.3.4
这就证明了它们在对应点的主法线以及从法线也分别平行而且它们的曲率与挠率也都成正比例.如果x(s)为一般螺线根据例1.3.4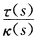 为常数故
为常数故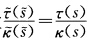 也为常数.再根据例1.3.4知
也为常数.再根据例1.3.4知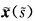 也为一般螺线.
也为一般螺线.
因为与x(s)在对应点的切线平行,故.根据Frenet公式,有由于所以从而有再根据Frenet公式,有综合上述,得到这就证明了它们在对应点的主法线以及从法线也分别平行,而且它们的曲率与挠率也都成正比例.如果x(s)为一般螺线,根据例1.3.4为常数,故也为常数.再根据例1.3.4知,也为一般螺线.
相似问题
设曲面M:x(u v)=(ucosv usinv lnu)与(Riemann流形基本定理)n维C∞R
设曲面M:x(u,v)=(ucosv,usinv,lnu)与(Riemann流形基本定理)n维C∞Riemann流形(M,g)=(M,(,>)上(Riemann流形基本定理)n维C∞Riemann流形(M,g)=(M,
设伪球面x(φ θ)=(acosφcosθ acosφsinθ a[ln(secφ+tanφ)一si
设伪球面x(φ,θ)=(acosφcosθ,acosφsinθ,a[ln(secφ+tanφ)一sinφ]) (a>0).证明:请帮忙给出正确答案和分析,谢谢!
在R3中曲面的一般参数下 证明:Gauss方程为KGF=(F121)u一(F111)v+F122F1
在R3中曲面的一般参数下,证明:Gauss方程为KGF=(F121)u一(F111)v+F122F121一F112F221,KGE=(F112)v一(F122)u+F111F122一F112F222一F12F1112一(F122)2,K
证明:在曲面M:x(u v)的一般参数u v下 弧长参数曲线(u(s) v(s))的测地曲率为 其中
证明:在曲面M:x(u,v)的一般参数u,v下,弧长参数曲线(u(s),v(s))的测地曲率为 其中A=A1=F111u2+2F121uv+F221v2,B=A2=F111u2请帮忙给出正确答案和分析,谢谢!
两条C3曲线设两条连通曲线与x之间建立了一一对应关系 使它们在对应点的主法线总是互相平行.证明:设两
两条C3曲线设两条连通曲线与x之间建立了一一对应关系,使它们在对应点的主法线总是互相平行.证明:设两条连通曲线与x之间建立了一一对应关系,使它们在












