在R3中曲面的一般参数下 证明：Gauss方程为KGF=(F121)u一(F111)v+F122F1

正确答案：(1)存Gauss方程(n=3)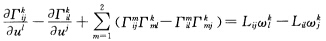：中取k=i=l=1J=2得到(F₁₂¹)_u^'一(F₁₁¹)_v^'+F₁₂²F₂₁¹一F₁₁²F₂₂¹=L₁₂ω₁¹—L₁₁ω₂¹=L₁₂(g¹¹L₁₁+g¹²L₂₁)一L₁₁(g¹¹L₁₂+g¹²L₂₂)=g¹²(L₁₂²一L₁₁L₂₂)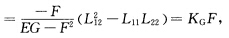其中由对称性立知第4式成立．或者仿上直接验证：取k=i=l=2j=1得到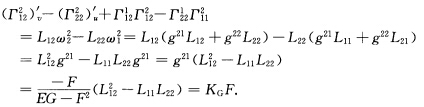取k=1=li=2=j得到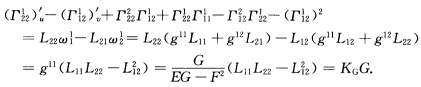由对称性立知第2式成立．或者仿上直接验证：取k=2=li=1=j得到(2)在Codazzi方程(n=3)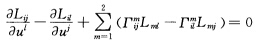：中取i=j=1l=2得到(L₁₁)_u^'一(L₁₂)_u^'+(F₁₁^'L₁₂一F₁₂¹L₁₁)+(F₁₁²L₂₂一F₁₂²L₂₁)=0即L_v^'一M_u^'=LF₁₂¹+M(F₁₂²一F₁₁¹)一NF₁₁²．由对称性立知第2式成立．或者仿上直接证明：取i=j=2l=1得到(L₂₂)_u^'一(L₂₁)₂^'+(F₂₂¹L₁₁一F₂₁¹L₁₂)+(F₂₂²L₂₁一F₂₁²L₂₂)=0即N_u^'一M_v^'+LF₂₂¹一MF₂₁¹+MF₂₂²一NF₂₁²=0M_v^'一N_u^'=LF₂₂¹+M(F₂₂²一F₁₂¹)一NF₁₂²．
(1)存Gauss方程(n=3)：中,取k=i=l=1,J=2,得到(F121)u'一(F111)v'+F122F211一F112F221=L12ω11—L11ω21=L12(g11L11+g12L21)一L11(g11L12+g12L22)=g12(L122一L11L22)其中由对称性立知第4式成立．或者仿上直接验证：取k=i=l=2,j=1,得到取k=1=l,i=2=j,得到由对称性立知第2式成立．或者仿上直接验证：取k=2=l,i=1=j,得到(2)在Codazzi方程(n=3)：中,取i=j=1,l=2,得到(L11)u'一(L12)u'+(F11'L12一F121L11)+(F112L22一F122L21)=0,即Lv'一Mu'=LF121+M(F122一F111)一NF112．由对称性立知第2式成立．或者仿上直接证明：取i=j=2,l=1,得到(L22)u'一(L21)2'+(F221L11一F211L12)+(F222L21一F212L22)=0,即Nu'一Mv'+LF221一MF211+MF222一NF212=0,Mv'一Nu'=LF221+M(F222一F121)一NF122．