I=ds2=[φ(u)+ψ(v)](du2+dv2)请帮忙给出正确答案和分析 谢谢！
I=ds2=[φ(u)+ψ(v)](du2+dv2)
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-16 21:25:01
正确答案：因为F=0故参数曲线为正交曲线网并且E=G=φ(u)+ψ(v)．根据例2．4．1
于是
代入一般参数下的测地线方程(参阅习题2．8．5)其中
于是测地线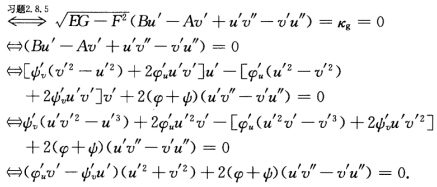
两边乘u'v'得
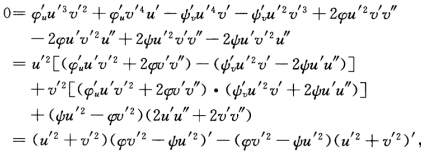或
从而可得
最后得到测地线的微分方程：[φ(u)+hdv2一[(ψv)一hdu2=0
因为F=0,故参数曲线为正交曲线网,并且E=G=φ(u)+ψ(v)．根据例2．4．1,于是代入一般参数下的测地线方程(参阅习题2．8．5),其中于是,测地线两边乘u'v',得或从而可得最后得到测地线的微分方程：[φ(u)+hdv2一[(ψv)一hdu2=0
相似问题
如果连通曲线x(s)(s∈(α β)为弧长)的所有密切平面都垂直于一条固定直线 证明：该曲线x(s)
如果连通曲线x(s)(s∈(α，β)为弧长)的所有密切平面都垂直于一条固定直线，证明：该曲线x(s)(α<s<β)必为平面曲线．请帮忙给出正确答案和分析，谢谢！
取整函数y＝[х] х∈(－∞ +∞)是否为初等函数?为什么?请帮忙给出正确答案和分析 谢谢！
取整函数y＝[х]，х∈(－∞，+∞)是否为初等函数?为什么?请帮忙给出正确答案和分析，谢谢！
若两条C4连通曲线可建立对应 使对应点的从法线重合 则这两条曲线或者重合 或者都是平面曲线．请帮忙给
若两条C4连通曲线可建立对应，使对应点的从法线重合，则这两条曲线或者重合，或者都是平面曲线．请帮忙给出正确答案和分析，谢谢！
设e1 e2 ω1 ω2和R3中任何C2极小曲面M上存在局部等温参数．R3中任何C2极小曲面M上存在
设e1，e2，ω1，ω2和R3中任何C2极小曲面M上存在局部等温参数．R3中任何C2极小曲面M上存在局部等温参数．请帮忙给出正确答案和分析，谢谢！
求双曲抛物面x(u v)=(a(u+v) b(u一v) 2uv)的曲率线方程．请帮忙给出正确答案和分
求双曲抛物面x(u，v)=(a(u+v)，b(u一v)，2uv)的曲率线方程．请帮忙给出正确答案和分析，谢谢！
