若两条C4连通曲线可建立对应 使对应点的从法线重合 则这两条曲线或者重合 或者都是平面曲线.请帮忙给
若两条C4连通曲线可建立对应,使对应点的从法线重合,则这两条曲线或者重合,或者都是平面曲线.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:证法1 由两曲线的从法线重合可设 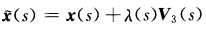 其中S为曲线x(s)的弧长而为另一曲线
其中S为曲线x(s)的弧长而为另一曲线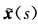 的参数未必为其弧长.对s求导得
的参数未必为其弧长.对s求导得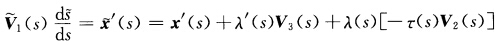 =V1(s)一λ(s)v(s)V2(s)+λ'(s)V3(s).因为
=V1(s)一λ(s)v(s)V2(s)+λ'(s)V3(s).因为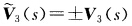 两边用V3(s)作内积得λ'(s)=0λ(s)=λ0(常数)x'(s)=V1(s)一λ0τ(s)V2(s).于是
两边用V3(s)作内积得λ'(s)=0λ(s)=λ0(常数)x'(s)=V1(s)一λ0τ(s)V2(s).于是 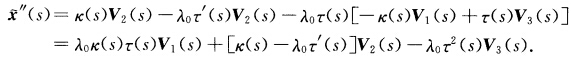 .因此
.因此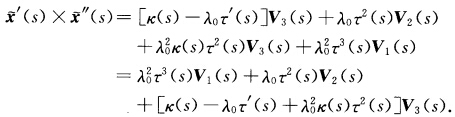 .这是公共的从法向即
.这是公共的从法向即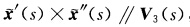 故λ0τ2(s)=0.如果
故λ0τ2(s)=0.如果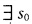 使得τ(s0)≠0则λ0=0.再由于λ(s)=λ0为常数故λ(s)=λ0≡0且
使得τ(s0)≠0则λ0=0.再由于λ(s)=λ0为常数故λ(s)=λ0≡0且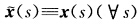 即这两曲线完全重合.如果τ(s)≡0(Vs)根据定理1.2.2x(s)为平面曲线.设曲线所在平面的单位法向为V3(s)=a.由于λ(s)≡λ0(常数Vs)故x'(s)=x(s)+λ(s)V3(s)=x(s)+λ0V3(s)=x(s)+λ0a.显然x(s)是将平面曲线x(s)向V3(s)=a方向平移λ0得到的所以它也是平面曲线.证法2依题意有
即这两曲线完全重合.如果τ(s)≡0(Vs)根据定理1.2.2x(s)为平面曲线.设曲线所在平面的单位法向为V3(s)=a.由于λ(s)≡λ0(常数Vs)故x'(s)=x(s)+λ(s)V3(s)=x(s)+λ0V3(s)=x(s)+λ0a.显然x(s)是将平面曲线x(s)向V3(s)=a方向平移λ0得到的所以它也是平面曲线.证法2依题意有 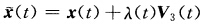 .两边关于t求导得
.两边关于t求导得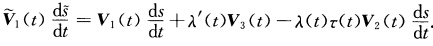 因为
因为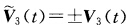 点乘(作内积)V3(t)得到λ'(t)=0 即 λ(t)=λ0(常数).从而由前式有
点乘(作内积)V3(t)得到λ'(t)=0 即 λ(t)=λ0(常数).从而由前式有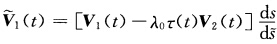 再对上式求导得
再对上式求导得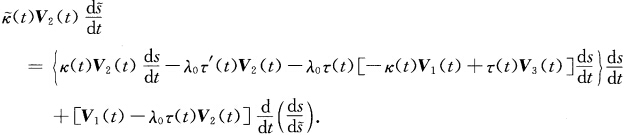 因为
因为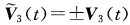 故点乘V3(t)得
故点乘V3(t)得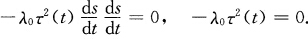 如果λ0=0则
如果λ0=0则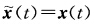 即两曲线重合.如果λ0≠0则τ(t)≡0.由完全与证法1相应部分相同的推导得两条曲线
即两曲线重合.如果λ0≠0则τ(t)≡0.由完全与证法1相应部分相同的推导得两条曲线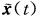 与x(t)都为平面曲线.
与x(t)都为平面曲线.
证法1由两曲线的从法线重合,可设,其中S为曲线x(s)的弧长,而为另一曲线的参数,未必为其弧长.对s求导,得=V1(s)一λ(s)v(s)V2(s)+λ'(s)V3(s).因为,两边用V3(s)作内积,得λ'(s)=0,λ(s)=λ0(常数),x'(s)=V1(s)一λ0τ(s)V2(s).于是.因此.这是公共的从法向,即,故λ0τ2(s)=0.如果,使得τ(s0)≠0,则λ0=0.再由于λ(s)=λ0为常数,故λ(s)=λ0≡0,且,即这两曲线完全重合.如果τ(s)≡0(Vs),根据定理1.2.2,x(s)为平面曲线.设曲线所在平面的单位法向为V3(s)=a.由于λ(s)≡λ0(常数,Vs),故x'(s)=x(s)+λ(s)V3(s)=x(s)+λ0V3(s)=x(s)+λ0a.显然,x(s)是将平面曲线x(s)向V3(s)=a方向平移λ0得到的,所以它也是平面曲线.证法2依题意有.两边关于t求导,得因为,点乘(作内积)V3(t),得到λ'(t)=0,即λ(t)=λ0(常数).从而由前式有再对上式求导,得因为故点乘V3(t),得如果λ0=0,则,即两曲线重合.如果λ0≠0,则τ(t)≡0.由完全与证法1相应部分相同的推导,得两条曲线与x(t)都为平面曲线.
相似问题
设e1 e2 ω1 ω2和R3中任何C2极小曲面M上存在局部等温参数.R3中任何C2极小曲面M上存在
设e1,e2,ω1,ω2和R3中任何C2极小曲面M上存在局部等温参数.R3中任何C2极小曲面M上存在局部等温参数.请帮忙给出正确答案和分析,谢谢!
求双曲抛物面x(u v)=(a(u+v) b(u一v) 2uv)的曲率线方程.请帮忙给出正确答案和分
求双曲抛物面x(u,v)=(a(u+v),b(u一v),2uv)的曲率线方程.请帮忙给出正确答案和分析,谢谢!
设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn|f(x)=0}≠∮ 且对设为Rn+1中的
设f(x)为Rn上的一个Cr函数(r≥1),M={x∈Rn|f(x)=0}≠∮,且对设为Rn+1中的n维Ck(k≥1)连通、正则子流形,设为Rn+1中的n维Ck(k≥1)连通、正则子流形,
对于R3中2维定向的闭曲面(紧致 无边的曲面) 有其中M+={P∈M|KG(P)≥0) g=g(M)
对于R3中2维定向的闭曲面(紧致、无边的曲面),有其中M+={P∈M|KG(P)≥0),g=g(M)为曲面M的亏格.请帮忙给出正确答案和分析,谢谢!
求悬链线用极坐标方程r=r(θ)给出曲线的弧长表达式 其中r(θ)为C1函数.用极坐标方程r=r(θ
求悬链线用极坐标方程r=r(θ)给出曲线的弧长表达式,其中r(θ)为C1函数.用极坐标方程r=r(θ)给出曲线的弧长表达式,其中r(θ)为C1函数.请帮忙给出正确












