设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn｜f(x)=0}≠∮ 且对设为Rn＋1中的
设f(x)为Rn上的一个Cr函数(r≥1)，M={x∈Rn｜f(x)=0}≠∮，且对设为Rn＋1中的n维Ck(k≥1)连通、正则子流形，
设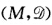
为Rn+1中的n维Ck(k≥1)连通、正则子流形，则下列各条等价： (1)M可定向；(2)M上存在连续变动的单位法向量场(
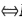M上存在连续变动的处处非零的法向量场)；(3)对M上任何闭曲线C，从C上的任一固定点P出发，一个单位法向量沿C连续变动，当回到P点时，单位法向量不变； (4)对
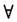P，Q∈M，C1与C2是从P到Q的任何两条曲线，一个单位法向量从P点出发分别沿C1，C2连续变动时，到达Q点，单位法向量相同．自然有它的对偶形式：(1’)M不可定向；(2’)M上不存在连续变动的单位法向量场(
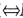M上不存在连续变动的处处非零的法向量场)．(3’)在M上存在一条闭曲线C，从C的某一点P出发，某个单位法向量沿C连续变动时，当回到P点时，单位法向量改变方向；(4’)存在P，Q∈M，C1与C2是从P到Q的某两条曲线，某个单位法向量从P点出发分别沿C1，C2连续变动时，到达Q点，单位法向量不同(即相反)．
请帮忙给出正确答案和分析，谢谢！
参考解答
406***102
2024-11-16 21:11:13
正确答案：(1)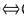
(2) 参阅[7第183页定理2或[8第328页定理11．2．1(2)→(3)显然.(3)←(4) 取C1=CC2=P(常值)的道路．显然沿C2=P(常值)的道路单位法向量不变由(4)沿Ci=C回到P时单位法向量也不变．(3)→(4) 令C=C2-1C1它是从P到P的闭曲线由(3)知单位法向量不变故一个单位法向量从P点出发分别沿C1C2连续变动时到达Q点单位法向量相同．(2)←(4) 在M上取定一点P由于M连通它等价于道路连通．对
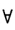Q∈M任作连接P与Q的道路C.P点处的一个单位法向量沿C连续变动得到Q点处的一个单位法向量．由(4)知它与道路C的选取无关．于是唯一决定了M上的一个单位法向量场1．因为n是沿曲线连续变动得到的显然从局部看n是连续的自然它也是M上的连续单位法向量场．
(1)(2)参阅[7第183页定理2或[8第328页定理11．2．1(2)→(3)显然.(3)←(4)取C1=C,C2=P(常值)的道路．显然,沿C2=P(常值)的道路,单位法向量不变,由(4)沿Ci=C,回到P时,单位法向量也不变．(3)→(4)令C=C2-1C1,它是从P到P的闭曲线,由(3)知单位法向量不变,故一个单位法向量从P点出发分别沿C1,C2连续变动时,到达Q点,单位法向量相同．(2)←(4)在M上取定一点P,由于M连通,它等价于道路连通．对Q∈M,任作连接P与Q的道路C.P点处的一个单位法向量沿C连续变动得到Q点处的一个单位法向量．由(4)知,它与道路C的选取无关．于是,唯一决定了M上的一个单位法向量场,1．因为n是沿曲线连续变动得到的,显然从局部看n是连续的,自然它也是M上的连续单位法向量场．
相似问题
对于R3中2维定向的闭曲面(紧致 无边的曲面) 有其中M+={P∈M｜KG(P)≥0) g=g(M)
对于R3中2维定向的闭曲面(紧致、无边的曲面)，有其中M+={P∈M｜KG(P)≥0)，g=g(M)为曲面M的亏格．请帮忙给出正确答案和分析，谢谢！
求悬链线用极坐标方程r=r(θ)给出曲线的弧长表达式 其中r(θ)为C1函数．用极坐标方程r=r(θ
求悬链线用极坐标方程r=r(θ)给出曲线的弧长表达式，其中r(θ)为C1函数．用极坐标方程r=r(θ)给出曲线的弧长表达式，其中r(θ)为C1函数．请帮忙给出正确
设函数f(x)在点x=a处可导 则甬数｜f(x)｜在点x=a处不可导的充分条件是( )．A．f(a)
设函数f(x)在点x=a处可导，则甬数｜f(x)｜在点x=a处不可导的充分条件是( )．A．f(a)=0且f"(a)=0B．f(a)=0且f"(a)≠0C．f(a)>0且f"(a)>0D．f(a)<0且f"(a)
求下列极限： 在平面3x－2z＝0上求一点 使它与点A(1 1 1)和点B(2 3 4)的距离平方和
求下列极限： 在平面3x－2z＝0上求一点，使它与点A(1，1，1)和点B(2，3，4)的距离平方和最小．在平面3x－2z＝0上求一点，使它与点A(1，1，1)和点B(2，3
设函数f(u)可导 y=f(x2)当自变量x在x=一1处取得增量△x=-0．1时 相应的函数增量△y
设函数f(u)可导，y=f(x2)当自变量x在x=一1处取得增量△x=-0．1时，相应的函数增量△y的线性主部为0．1，则f(1)=( )．A．一1B．0．1C．1D．0．5请帮忙给
