对于R3中2维定向的闭曲面(紧致 无边的曲面) 有其中M+={P∈M｜KG(P)≥0) g=g(M)
对于R3中2维定向的闭曲面(紧致、无边的曲面)，有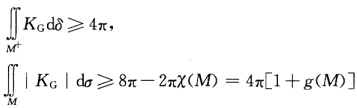
其中M+={P∈M｜KG(P)≥0)，g=g(M)为曲面M的亏格．
请帮忙给出正确答案和分析，谢谢！
参考解答
481***102
2024-11-16 21:05:28
正确答案：再记M-={P∈Ml KG(P)<0)并考察习题3．3．9的证明可知那里得到的函数f的最大值点与最小值点P1P2中每个点都不可能是双曲点它的两个主曲率必须同号故KG(Pi)≥0(i=12)．这表明限制到M+上Gauss映射已经是满射．因此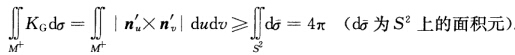
于是再由X(M)=2[1一g(M得到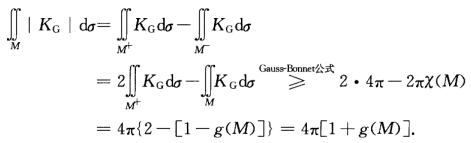
再记M-={P∈MlKG(P)<0),并考察习题3．3．9的证明可知,那里得到的函数f的最大值点与最小值点P1,P2中每个点都不可能是双曲点,它的两个主曲率必须同号,故KG(Pi)≥0(i=1,2)．这表明限制到M+上,Gauss映射已经是满射．因此于是,再由X(M)=2[1一g(M,得到
相似问题
求悬链线用极坐标方程r=r(θ)给出曲线的弧长表达式 其中r(θ)为C1函数．用极坐标方程r=r(θ
求悬链线用极坐标方程r=r(θ)给出曲线的弧长表达式，其中r(θ)为C1函数．用极坐标方程r=r(θ)给出曲线的弧长表达式，其中r(θ)为C1函数．请帮忙给出正确
设函数f(x)在点x=a处可导 则甬数｜f(x)｜在点x=a处不可导的充分条件是( )．A．f(a)
设函数f(x)在点x=a处可导，则甬数｜f(x)｜在点x=a处不可导的充分条件是( )．A．f(a)=0且f"(a)=0B．f(a)=0且f"(a)≠0C．f(a)>0且f"(a)>0D．f(a)<0且f"(a)
求下列极限： 在平面3x－2z＝0上求一点 使它与点A(1 1 1)和点B(2 3 4)的距离平方和
求下列极限： 在平面3x－2z＝0上求一点，使它与点A(1，1，1)和点B(2，3，4)的距离平方和最小．在平面3x－2z＝0上求一点，使它与点A(1，1，1)和点B(2，3
设函数f(u)可导 y=f(x2)当自变量x在x=一1处取得增量△x=-0．1时 相应的函数增量△y
设函数f(u)可导，y=f(x2)当自变量x在x=一1处取得增量△x=-0．1时，相应的函数增量△y的线性主部为0．1，则f(1)=( )．A．一1B．0．1C．1D．0．5请帮忙给
求下列函数的二阶偏导数：计算下列二重积分：计算下列二重积分： 请帮忙给出正确答案和分析 谢谢！
求下列函数的二阶偏导数：计算下列二重积分：计算下列二重积分： 请帮忙给出正确答案和分析，谢谢！
