求悬链线用极坐标方程r=r(θ)给出曲线的弧长表达式 其中r(θ)为C1函数．用极坐标方程r=r(θ
求悬链线用极坐标方程r=r(θ)给出曲线的弧长表达式，其中r(θ)为C1函数．
用极坐标方程r=r(θ)给出曲线的弧长表达式，其中r(θ)为C1函数．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***102
2024-11-16 20:55:59
正确答案：解法1计算得x(θ)=(r(θ)cosθr(θ)sinθ)x'(θ)=(r'(θ)cosθ—r(θ)sinθr'(θ)sinθ+r(θ)cosθ)．弧长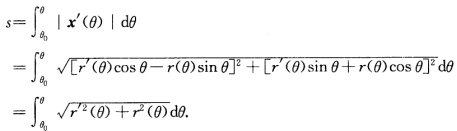
解法2 曲线极坐标方程r=r(θ)写成复数形式为Z=r(θ)eiθ则有dZ=eiθdr+ireiθdθ=eiθ[r'(θ)+ir(θ)dθ．弧长元
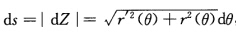故弧长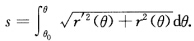
解法1计算得x(θ)=(r(θ)cosθ,r(θ)sinθ),x'(θ)=(r'(θ)cosθ—r(θ)sinθ,r'(θ)sinθ+r(θ)cosθ)．弧长解法2曲线极坐标方程r=r(θ),写成复数形式为Z=r(θ)eiθ,则有dZ=eiθdr+ireiθdθ=eiθ[r'(θ)+ir(θ)dθ．弧长元故弧长
相似问题
设函数f(x)在点x=a处可导 则甬数｜f(x)｜在点x=a处不可导的充分条件是( )．A．f(a)
设函数f(x)在点x=a处可导，则甬数｜f(x)｜在点x=a处不可导的充分条件是( )．A．f(a)=0且f"(a)=0B．f(a)=0且f"(a)≠0C．f(a)>0且f"(a)>0D．f(a)<0且f"(a)
求下列极限： 在平面3x－2z＝0上求一点 使它与点A(1 1 1)和点B(2 3 4)的距离平方和
求下列极限： 在平面3x－2z＝0上求一点，使它与点A(1，1，1)和点B(2，3，4)的距离平方和最小．在平面3x－2z＝0上求一点，使它与点A(1，1，1)和点B(2，3
设函数f(u)可导 y=f(x2)当自变量x在x=一1处取得增量△x=-0．1时 相应的函数增量△y
设函数f(u)可导，y=f(x2)当自变量x在x=一1处取得增量△x=-0．1时，相应的函数增量△y的线性主部为0．1，则f(1)=( )．A．一1B．0．1C．1D．0．5请帮忙给
求下列函数的二阶偏导数：计算下列二重积分：计算下列二重积分： 请帮忙给出正确答案和分析 谢谢！
求下列函数的二阶偏导数：计算下列二重积分：计算下列二重积分： 请帮忙给出正确答案和分析，谢谢！
设f(x)为连续函数 且F(x)则f(x)等于( )．A．B．C．D．请帮忙给出正确答案和分析 谢谢
设f(x)为连续函数，且F(x)则f(x)等于( )．A．B．C．D．请帮忙给出正确答案和分析，谢谢！
