设曲面M:x(u v)=(ucosv usinv lnu)与(Riemann流形基本定理)n维C∞R
设曲面M:x(u,v)=(ucosv,usinv,lnu)与(Riemann流形基本定理)n维C∞Riemann流形(M,g)=(M,(,>)上
(Riemann流形基本定理)n维C∞Riemann流形(M,g)=(M,(,>)上存在唯一的Riemann联络.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(近代观点、不变观点或映射观点) 先证唯一性.设▽及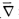 都是 (Mg)=(M(>)的Riemann联络.则X
都是 (Mg)=(M(>)的Riemann联络.则X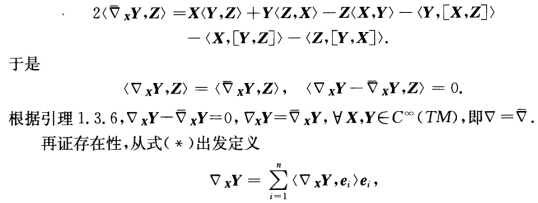 其中{ei为局部C∞规范正交基向量场而(▽XYei>按公式(*)给出.如果
其中{ei为局部C∞规范正交基向量场而(▽XYei>按公式(*)给出.如果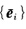 为另一局部C∞规范正交基向量场则
为另一局部C∞规范正交基向量场则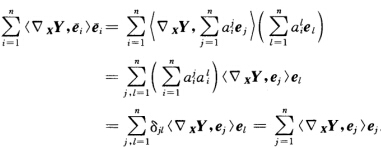 也就是公式(*)与局部C∞规范正交基的选取无关故▽XY确实定义了一个整体C∞切向量场.由Z的任意性通过式(*)作简单的运算可知▽满足线性联络的3个条件.此外由于
也就是公式(*)与局部C∞规范正交基的选取无关故▽XY确实定义了一个整体C∞切向量场.由Z的任意性通过式(*)作简单的运算可知▽满足线性联络的3个条件.此外由于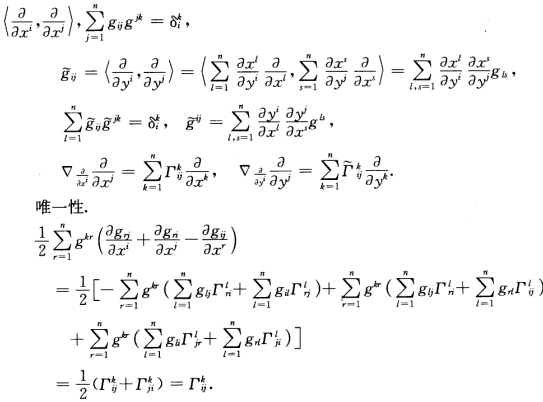 2<▽XY—▽YX—[XYZ>={X
2<▽XY—▽YX—[XYZ>={X
(近代观点、不变观点或映射观点)先证唯一性.设▽及都是(M,g)=(M,(,>)的Riemann联络.则XXY,Z)+(Y,▽XZ>+<▽YZ,X>+(Z,▽YX>一<▽ZX,Y>一(X,▽ZY>=(▽XY,Z>+(Y,[X,Z>+([Y,Z,X>+(Z,▽XY>+(Z,[Y,X>2(▽XY,Z>=X=(Y,[X,Z>一(X,[Y,Z>一(Z,[Y,X>.(*)同理其中{ei为局部C∞规范正交基向量场,而(▽XY,ei>按公式(*)给出.如果为另一局部C∞规范正交基向量场,则也就是公式(*)与局部C∞规范正交基的选取无关,故▽XY确实定义了一个整体C∞切向量场.由Z的任意性,通过式(*)作简单的运算,可知▽满足线性联络的3个条件.此外,由于2<▽XY—▽YX—[X,Y,Z>={X一Z一(Z,[Y,X>一{Y+X一z一(X,Y,Z>一(Y,[X,Z>一(Z,[X,Y>)一2([X,Y,Z>=0,又由于Z任意,特别地Z=▽XY-▽YX一[X,Y,所以T=▽XY—▽YX一[X,Y=0,即▽满足(4).另有2<▽ZXY>+2<▽ZY,X)={Z(X,Y>+X(Y,Z>Y一(X,[Z,Y>一+(Z+Y一X一一(Z,[Y,X>一=2Z,即Z=(▽ZX,Y>+(x,▽ZY>,这就证明了▽满足(5).
相似问题
设伪球面x(φ θ)=(acosφcosθ acosφsinθ a[ln(secφ+tanφ)一si
设伪球面x(φ,θ)=(acosφcosθ,acosφsinθ,a[ln(secφ+tanφ)一sinφ]) (a>0).证明:请帮忙给出正确答案和分析,谢谢!
在R3中曲面的一般参数下 证明:Gauss方程为KGF=(F121)u一(F111)v+F122F1
在R3中曲面的一般参数下,证明:Gauss方程为KGF=(F121)u一(F111)v+F122F121一F112F221,KGE=(F112)v一(F122)u+F111F122一F112F222一F12F1112一(F122)2,K
证明:在曲面M:x(u v)的一般参数u v下 弧长参数曲线(u(s) v(s))的测地曲率为 其中
证明:在曲面M:x(u,v)的一般参数u,v下,弧长参数曲线(u(s),v(s))的测地曲率为 其中A=A1=F111u2+2F121uv+F221v2,B=A2=F111u2请帮忙给出正确答案和分析,谢谢!
两条C3曲线设两条连通曲线与x之间建立了一一对应关系 使它们在对应点的主法线总是互相平行.证明:设两
两条C3曲线设两条连通曲线与x之间建立了一一对应关系,使它们在对应点的主法线总是互相平行.证明:设两条连通曲线与x之间建立了一一对应关系,使它们在
I=ds2=[φ(u)+ψ(v)](du2+dv2)请帮忙给出正确答案和分析 谢谢!
I=ds2=[φ(u)+ψ(v)](du2+dv2)请帮忙给出正确答案和分析,谢谢!












