设f(x)为Rn上的一个Cr函数(r≥1) M={x∈Rn|f(x)=0}≠∮ 且对证明:R3中环面
设f(x)为Rn上的一个Cr函数(r≥1),M={x∈Rn|f(x)=0}≠∮,且对证明:R3中环面T2是可定向的.
证明:R3中环面T2是可定向的.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:证法1环面的参数表示为x(uv)=((a+rcosu)cosv(a+rcosu)sinvrsinu)其中0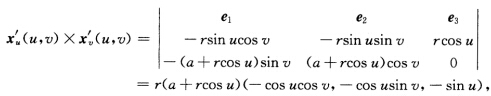 单位法向量
单位法向量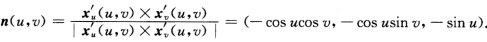 显然n(uv)为环面T2上的整体C∞单位法向量场根据习题3.1.3(2)知环面T2是可定向的.证法2考察上述环面T2的参数表示选以(iπjπ)(ij=0±1)为中心、2π为边长的开正方形它对应环面的开集作为T2上的局部坐标邻域共9个覆盖了整个环面其中凡有非空交集的任何两个它们的局部坐标分别记为{uv
显然n(uv)为环面T2上的整体C∞单位法向量场根据习题3.1.3(2)知环面T2是可定向的.证法2考察上述环面T2的参数表示选以(iπjπ)(ij=0±1)为中心、2π为边长的开正方形它对应环面的开集作为T2上的局部坐标邻域共9个覆盖了整个环面其中凡有非空交集的任何两个它们的局部坐标分别记为{uv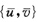 必有
必有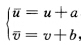 其中ab=±π.因此
其中ab=±π.因此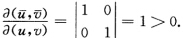 根据定义3.1.2环面是可定向的.证法3 因为
根据定义3.1.2环面是可定向的.证法3 因为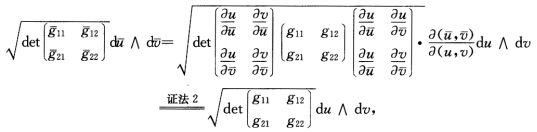 所以9个局部C∞单位体积元素(2维情形也称为面积元)
所以9个局部C∞单位体积元素(2维情形也称为面积元)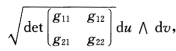 形(拼)成了环面T2上的C∞单位体积元素.根据习题3.1-3注(2)环面T2是可定向的.
形(拼)成了环面T2上的C∞单位体积元素.根据习题3.1-3注(2)环面T2是可定向的.
证法1环面的参数表示为x(u,v)=((a+rcosu)cosv,(a+rcosu)sinv,rsinu),其中0u'(u,v)=(一rsinucosv,一rsinusinv,rcosu),xv'(u,v)=(一(a+rcosu)sinv,(a+rcosu)cosv,0),单位法向量显然,n(u,v)为环面T2上的整体C∞单位法向量场,根据习题3.1.3(2)知,环面T2是可定向的.证法2考察上述环面T2的参数表示,选以(iπ,jπ)(i,j=0,±1)为中心、2π为边长的开正方形,它对应环面的开集作为T2上的局部坐标邻域,共9个覆盖了整个环面,其中凡有非空交集的任何两个,它们的局部坐标分别记为{u,v,,必有其中a,b=±π.因此根据定义3.1.2,环面是可定向的.证法3因为所以,9个局部C∞单位体积元素(2维情形也称为面积元)形(拼)成了环面T2上的C∞单位体积元素.根据习题3.1-3注(2),环面T2是可定向的.
相似问题
求悬链面M:上的渐近曲线.请帮忙给出正确答案和分析 谢谢!
求悬链面M:上的渐近曲线.请帮忙给出正确答案和分析,谢谢!
证明:Mbbius带是不可定向的.请帮忙给出正确答案和分析 谢谢!
证明:Mbbius带是不可定向的.请帮忙给出正确答案和分析,谢谢!
对于R3中2维定向光滑闭曲面(紧致 无边的曲面称为闭曲面)M Gauss映射G:M→S2为满射.请帮
对于R3中2维定向光滑闭曲面(紧致、无边的曲面称为闭曲面)M,Gauss映射G:M→S2为满射.请帮忙给出正确答案和分析,谢谢!
两条C3曲线与x(s)之间建立了一一对应关系 使它们在对应点的切线平行. 证明:它们在对应点的主法线
两条C3曲线与x(s)之间建立了一一对应关系,使它们在对应点的切线平行. 证明:它们在对应点的主法线以及从法线也分别平行,而且它们的曲率与挠率也都成
设曲面M:x(u v)=(ucosv usinv lnu)与(Riemann流形基本定理)n维C∞R
设曲面M:x(u,v)=(ucosv,usinv,lnu)与(Riemann流形基本定理)n维C∞Riemann流形(M,g)=(M,(,>)上(Riemann流形基本定理)n维C∞Riemann流形(M,g)=(M,












