参考解答
正确答案:解法1 由例2.7.4知 即得.解法2 由例2.7.4悬链面M为旋转曲面.再从例2.3.3及
即得.解法2 由例2.7.4悬链面M为旋转曲面.再从例2.3.3及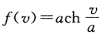 g(v)=v有g'(v)=1g''(v)=0
g(v)=v有g'(v)=1g''(v)=0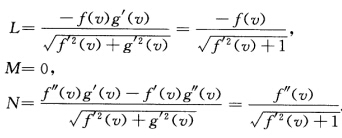 于是渐近曲线 Ldu2+2Mdudv+Ndv2=0
于是渐近曲线 Ldu2+2Mdudv+Ndv2=0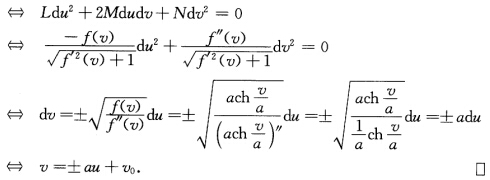
解法1由例2.7.4,知即得.解法2由例2.7.4,悬链面M为旋转曲面.再从例2.3.3及,g(v)=v,有g'(v)=1,g''(v)=0,于是渐近曲线Ldu2+2Mdudv+Ndv2=0
相似问题
证明:Mbbius带是不可定向的.请帮忙给出正确答案和分析 谢谢!
证明:Mbbius带是不可定向的.请帮忙给出正确答案和分析,谢谢!
对于R3中2维定向光滑闭曲面(紧致 无边的曲面称为闭曲面)M Gauss映射G:M→S2为满射.请帮
对于R3中2维定向光滑闭曲面(紧致、无边的曲面称为闭曲面)M,Gauss映射G:M→S2为满射.请帮忙给出正确答案和分析,谢谢!
两条C3曲线与x(s)之间建立了一一对应关系 使它们在对应点的切线平行. 证明:它们在对应点的主法线
两条C3曲线与x(s)之间建立了一一对应关系,使它们在对应点的切线平行. 证明:它们在对应点的主法线以及从法线也分别平行,而且它们的曲率与挠率也都成
设曲面M:x(u v)=(ucosv usinv lnu)与(Riemann流形基本定理)n维C∞R
设曲面M:x(u,v)=(ucosv,usinv,lnu)与(Riemann流形基本定理)n维C∞Riemann流形(M,g)=(M,(,>)上(Riemann流形基本定理)n维C∞Riemann流形(M,g)=(M,
设伪球面x(φ θ)=(acosφcosθ acosφsinθ a[ln(secφ+tanφ)一si
设伪球面x(φ,θ)=(acosφcosθ,acosφsinθ,a[ln(secφ+tanφ)一sinφ]) (a>0).证明:请帮忙给出正确答案和分析,谢谢!


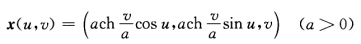 上的渐近曲线.
上的渐近曲线.









