求证：有心二次曲线的互相垂直的切线的交点的轨迹是一个与二次曲线同心的圆．请帮忙给出正确答案和分析 谢

正确答案：如图2—6一14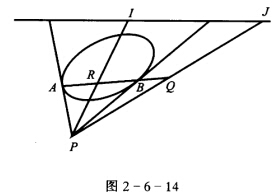． 设有心二次曲线的互相垂直的切线的交点为PPIPJ为过P点的迷向直线根据拉盖尔定理知P(ABU)＝－1设PI交AB于RPJ交AB于Q则(ABRQ)＝－1所以RQ是共轭点PIPJ是共轭直线当P点变动时线束J(P)线束J(P)所以P点的轨迹是一条二次曲线S′又S′过I、J因而S′是一个圆． 再证明S′与原二次曲线S同心． 如图2—6—15作二次曲S的外切矩形P₁P₂P₃P₄因为P₁P₂P₃P₄都是垂直切线的交点所以它们都在圆S′上且其对角线P₁P₃与P₂P₄的交点O是圆S′的中心设P₁P₂与P₃P₄交于V_∞P₁P₄与P₂P₃交于U_∞根据布利安桑定理与完全四线形的调和性知O为l_∞的极点．所以O是原二次曲线S的中心．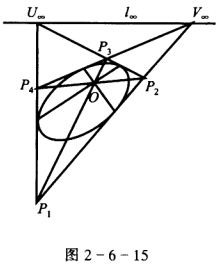
如图2—6一14．设有心二次曲线的互相垂直的切线的交点为P,PI,PJ为过P点的迷向直线,根据拉盖尔定理知P(AB,U)＝－1,设PI交AB于R,PJ交AB于Q,则(AB,RQ)＝－1,所以R,Q是共轭点,PI,PJ是共轭直线,当P点变动时,线束J(P)线束J(P),所以P点的轨迹是一条二次曲线S′,又S′过I、J因而S′是一个圆．再证明S′与原二次曲线S同心．如图2—6—15,作二次曲S的外切矩形P1P2P3P4,因为P1,P2,P3,P4都是垂直切线的交点,所以它们都在圆S′上,且其对角线P1P3与P2P4的交点O是圆S′的中心,设P1P2与P3P4交于V∞,P1P4与P2P3交于U∞,根据布利安桑定理与完全四线形的调和性,知O为l∞的极点．所以O是原二次曲线S的中心．