设随机变量X与Y独立 且都服从N(μ σ2) 求E[max(X Y)] E[min(X Y)]．请帮

参考解答

470***444

2023-11-13 20:39:53



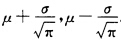
相似问题

• 设离散型随机变量X服从巴斯卡分布 其分布律为 P{X=k)=Ck—1r—1prqk—r k=r r+

  设离散型随机变量X服从巴斯卡分布，其分布律为 P{X=k)=Ck—1r—1prqk—r，k=r，r+1，r+2，…，0＜p＜1，q=1一p，其中r＞0为已知正整数，求E(X)和D(X)．

• 对于随机变量X Y Z 若已知 E(X)=E(Y)=一1 E(Z)=1 D(X)=D(Y)=D(Z)

  对于随机变量X，Y，Z，若已知 E(X)=E(Y)=一1，E(Z)=1，D(X)=D(Y)=D(Z)=4， 求E(X+Y+Z)，D(X+Y+Z)．请帮忙给出正确答案和分析，谢谢！

• 设随机变量X的概率密度为 求E[min(｜X｜ 1)]和D[min(｜X｜ 1)]．请帮忙给出正确答

  设随机变量X的概率密度为，求E[min(｜X｜，1)]和D[min(｜X｜，1)]．请帮忙给出正确答案和分析，谢谢！

• 设随机变量(X Y)的分布律为 求：(1)当X=1时 Y的条件分布律及条件分布函数； (2)当Y=

  设随机变量(X，Y)的分布律为 求：(1)当X=1时，Y的条件分布律及条件分布函数； (2)当Y=0时，X的条件分布律及条件分布函数．请帮忙给出正确答案和分析，谢谢！

• 设三维随机变量(X Y Z)的概率密度为 证明：X与Z独立 Y与Z独立 而X与Y不独立．请帮忙给出

  设三维随机变量(X，Y，Z)的概率密度为 证明：X与Z独立，Y与Z独立，而X与Y不独立．请帮忙给出正确答案和分析，谢谢！