设三维随机变量(X Y Z)的概率密度为 证明：X与Z独立 Y与Z独立 而X与Y不独立．请帮忙给出
设三维随机变量(X，Y，Z)的概率密度为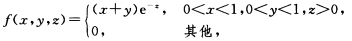 
证明：X与Z独立，Y与Z独立，而X与Y不独立．
请帮忙给出正确答案和分析，谢谢！
参考解答
492***444
2023-11-13 20:17:19
正确答案：为证X与Z独立先计算关于(XZ)的边缘概率密度fXZ(xz)．
由以上计算的结果容易看到对fX(xz)fX(x)fZ(z)的一切连续点(xz)有fXZ(xz)=fX(x)fZ(z)可见X与Z独立． 类似可以算得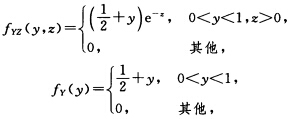
可见对fYZ(yz)fY(y)fZ(z)的一切连续点(yz)有fYZ(yz)=fY(y)fZ(z)可见Y与Z独立．最后由计算得
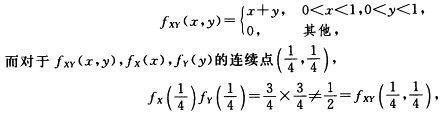即知X与Y不独立．
要证明X与Z独立，先利用计算(X，Z)的概率密度，再利用计算fX(x)，fZ(z)，然后验证对一切连续点是否有fXZ(x，z)=fX(x)fZ(z)．其他二结论的证明类似．不过在计算边缘概率密度时要注意的是，f(x，y，z)是分区域定义的，要分区域计算fXZ(x，z)，分段计算fX(x)和fZ(z)．
相似问题
设随机变量X与Y独立 且X～N(μ σ2) Y～N(μ σ2) 则Z—X+2Y+1～( )．A．N(
设随机变量X与Y独立，且X～N(μ，σ2)，Y～N(μ，σ2)，则Z—X+2Y+1～( )．A．N(μ1+μ2，σ12+4σ22)B．N(μ1+2μ2+1，σ12+4σ22)C．N(μ1+2μ2，σ12
已知随机变量(X1 X2 X3)的协方差矩阵为 设Y1=2X1+3X2+X3 Y2=X1一2X2+
已知随机变量(X1，X2，X3)的协方差矩阵为 设Y1=2X1+3X2+X3，Y2=X1一2X2+5X3，Y3=X2一X3，求(Y1，Y2，Y3)的协方差矩阵C*．请帮忙给出正确答案和分析，谢谢！
某灯泡厂生产的灯泡的平均寿命原为2 000小时 标准差为250小时．采用一项新工艺后使得平均寿命提高
某灯泡厂生产的灯泡的平均寿命原为2 000小时，标准差为250小时．采用一项新工艺后使得平均寿命提高到2 250小时，标准差不变．为了确认这一新工艺的效果
设二维随机变量(X Y)的概率密度为 求Z=X—Y的概率密度．请帮忙给出正确答案和分析 谢谢！
设二维随机变量(X，Y)的概率密度为 求Z=X—Y的概率密度．请帮忙给出正确答案和分析，谢谢！
设随机变量X1 X2 … Xn(n≥2)独立同分布 且概率密度为 求：(1)M=max(X1 X2
设随机变量X1，X2，…，Xn(n≥2)独立同分布，且概率密度为 求：(1)M=max(X1，X2，…，Xn)；(2)N=min(X1，X2，…，X3)的概率密度．请帮忙给出正确答案和分析，谢谢！
