某灯泡厂生产的灯泡的平均寿命原为2 000小时 标准差为250小时．采用一项新工艺后使得平均寿命提高
某灯泡厂生产的灯泡的平均寿命原为2 000小时，标准差为250小时．采用一项新工艺后使得平均寿命提高到2 250小时，标准差不变．为了确认这一新工艺的效果，技术部门要派人来检查，办法如下：任意抽取若干只灯泡作寿命试验，若这些灯泡的平均寿命超过2 200小时，就承认该新工艺有效．用中心极限定理计算，求任意抽取100只灯泡作寿命试验，新工艺得以通过的概率．如要使确认新工艺得以通过的概率不低于0．975，问至少要检查多少只灯泡?
请帮忙给出正确答案和分析，谢谢！
参考解答
4j5***444
2023-11-13 20:04:55
正确答案：令Xi=12…n表示采用新工艺后抽查的第i个灯泡的寿命则Xi=12…n独立同分布且E(X)=μ=2 250D(X)=σ2=2502．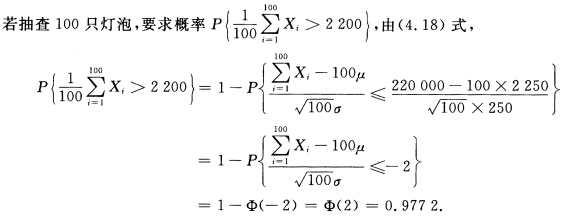
如要使确认新工艺得以通过的概率不低于0．975求至少要检查的灯泡数就是求最小的n使得
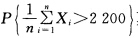≥0．975由(4．18)式 
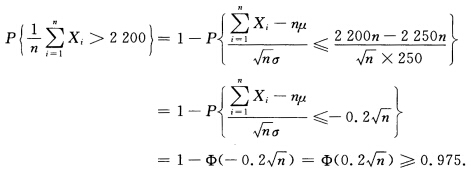查附表2知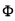
(1．96)=0．975于是应有0．2
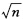≥1．96．解此不等式得n≥96．04即至少要检验97只灯泡才能使新工艺得以通过的概率不低于0．975．
令X,i=1,2,…,n表示采用新工艺后,抽查的第i个灯泡的寿命,则X,i=1,2,…,n独立同分布,且E(X)=μ=2250,D(X)=σ2=2502．如要使确认新工艺得以通过的概率不低于0．975,求至少要检查的灯泡数,就是求最小的n,使得≥0．975,由(4．18)式,查附表2,知(1．96)=0．975,于是应有0．2≥1．96．解此不等式,得n≥96．04,即至少要检验97只灯泡,才能使新工艺得以通过的概率不低于0．975．
相似问题
设二维随机变量(X Y)的概率密度为 求Z=X—Y的概率密度．请帮忙给出正确答案和分析 谢谢！
设二维随机变量(X，Y)的概率密度为 求Z=X—Y的概率密度．请帮忙给出正确答案和分析，谢谢！
设随机变量X1 X2 … Xn(n≥2)独立同分布 且概率密度为 求：(1)M=max(X1 X2
设随机变量X1，X2，…，Xn(n≥2)独立同分布，且概率密度为 求：(1)M=max(X1，X2，…，Xn)；(2)N=min(X1，X2，…，X3)的概率密度．请帮忙给出正确答案和分析，谢谢！
设加工出来的正圆锥形物件的高X和底圆直径Y是相互独立的随机变量 它们的概率密度分别为 求加工出来的
设加工出来的正圆锥形物件的高X和底圆直径Y是相互独立的随机变量，它们的概率密度分别为 求加工出来的正圆锥形物件的体积V的平均值．请帮忙给出正确答
设二维连续型随机变量(X Y)的概率密度为 求：(1)E(X)；(2)E(y)；(3)E(XY)；
设二维连续型随机变量(X，Y)的概率密度为 求：(1)E(X)；(2)E(y)；(3)E(XY)；(4)E(XY2)．请帮忙给出正确答案和分析，谢谢！
设随机变量Y的概率密度为 当Y=y(0＜y＜1)时 X的条件概率密度为 求：(X Y)的概率密度
设随机变量Y的概率密度为 当Y=y(0＜y＜1)时，X的条件概率密度为 求：(X，Y)的概率密度f(x，y)，P{x＞}．请帮忙给出正确答案和分析，谢谢！
