证明:一个正规矩阵若是三角矩阵 则它一定是对角矩阵.请帮忙给出正确答案和分析 谢谢!
证明:一个正规矩阵若是三角矩阵,则它一定是对角矩阵.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由A= 为正规矩阵必有AAT=ATA成立又
为正规矩阵必有AAT=ATA成立又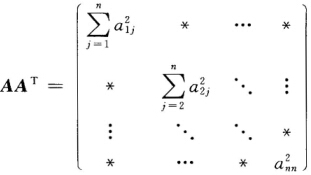
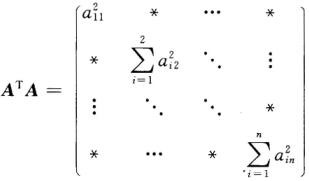 推得αij=0
推得αij=0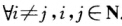
由A=为正规矩阵,必有AAT=ATA成立,又推得αij=0,
相似问题
设A∈Cm×n P Q分别是m阶和n阶可逆矩阵. (1)证明Q-1A-P-1∈(PAQ){1}; (
设A∈Cm×n,P,Q分别是m阶和n阶可逆矩阵. (1)证明Q-1A-P-1∈(PAQ){1}; (2)举例说明(PAQ)+=Q-1A+P-1不真.请帮忙给出正确答案和分析,谢谢!
设x Ax的向量范数为∥.∥2 证明:它对应的算子范数是证 对任意矩阵A 存在酉矩阵u V 使得矩阵
设x,Ax的向量范数为∥ ∥2,证明:它对应的算子范数是证 对任意矩阵A,存在酉矩阵u,V,使得矩阵A的奇异值分解为A=UDV.其中σ1,σ2,…,σn是矩阵A
证明R(A)=1的充分必要条件是存在非零列向量a和非零行向量bT 使A=ab1.请帮忙给出正确答案和
证明R(A)=1的充分必要条件是存在非零列向量a和非零行向量bT,使A=ab1.请帮忙给出正确答案和分析,谢谢!
如果n阶行列式中等于零的元素个数大于n2一n 那么行列式的值为_________.请帮忙给出正确答案
如果n阶行列式中等于零的元素个数大于n2一n,那么行列式的值为_________ 请帮忙给出正确答案和分析,谢谢!
设n阶矩阵A与s阶矩阵B都可逆 求:请帮忙给出正确答案和分析 谢谢!
设n阶矩阵A与s阶矩阵B都可逆,求:请帮忙给出正确答案和分析,谢谢!












