设x Ax的向量范数为∥.∥2 证明:它对应的算子范数是证 对任意矩阵A 存在酉矩阵u V 使得矩阵
设x,Ax的向量范数为∥.∥2,证明:它对应的算子范数是证 对任意矩阵A,存在酉矩阵u,V,使得矩阵A的奇异值分解为A=UDV.其中σ1,σ2,…,σn是矩阵A的奇异值,D=diag(σ1,σ2,…,σn).
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:根据定义有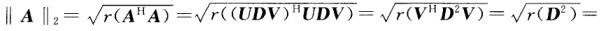 max{σ1σ2…σn.
max{σ1σ2…σn.
根据定义有max{σ1,σ2,…,σn.
相似问题
证明R(A)=1的充分必要条件是存在非零列向量a和非零行向量bT 使A=ab1.请帮忙给出正确答案和
证明R(A)=1的充分必要条件是存在非零列向量a和非零行向量bT,使A=ab1.请帮忙给出正确答案和分析,谢谢!
如果n阶行列式中等于零的元素个数大于n2一n 那么行列式的值为_________.请帮忙给出正确答案
如果n阶行列式中等于零的元素个数大于n2一n,那么行列式的值为_________ 请帮忙给出正确答案和分析,谢谢!
设n阶矩阵A与s阶矩阵B都可逆 求:请帮忙给出正确答案和分析 谢谢!
设n阶矩阵A与s阶矩阵B都可逆,求:请帮忙给出正确答案和分析,谢谢!
一水平浅色长传送带上放置一煤块(可视为质点) 煤块与传送带之间的动摩擦因数为μ。初始时 传送带与煤块
一水平浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ。初始时,传送带与煤块都是静止的。现让传送带以恒定的加速度a0开始运
我国《海商法》规定 在当事人没有约定的情况下 负责对被抵押船舶进行保险 并负担保险费的人是( )A
我国《海商法》规定,在当事人没有约定的情况下,负责对被抵押船舶进行保险,并负担保险费的人是( )A、抵押人B、抵押权人C、保险人D、提供贷款的银行












