求圆柱螺线的切向量 切线 主法线 密切平面 法平面方程.请帮忙给出正确答案和分析 谢谢!
求圆柱螺线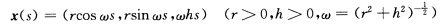 的切向量、切线、主法线、密切平面、法平面方程.
的切向量、切线、主法线、密切平面、法平面方程.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:由例1.1.3知V1(s)=x'(s)=w(-rsin(wsrcoswsh) (切向量s为弧长)且 k(s)V2(s)一V1'(s)=ω2(一rcosωs一rsinωs0)V2(s)=一(cos ωssin ωs0)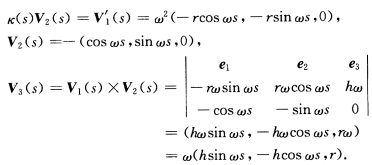 切线方程(方向为V1(s))为
切线方程(方向为V1(s))为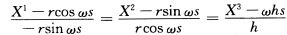 主法线方程(方向为V2(s))为
主法线方程(方向为V2(s))为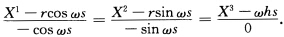 密切平面方程(平面法向为V3(s))为hsinωs(X1一rcosωs)一hcosωs(X2一rsincos)+r(X3一ωhs)=0即hsinωsX1一hcosωsX2+rX3一rwhs=0.法平面方程(平面法向为V1(s))为一rsinωs(X1一rcosωs)+rcosωs(X2一rsin ωs)+h(X3一ωhs)=0即 一rsinωsX1+rcosωsX2+hX3一ωh2s=0.
密切平面方程(平面法向为V3(s))为hsinωs(X1一rcosωs)一hcosωs(X2一rsincos)+r(X3一ωhs)=0即hsinωsX1一hcosωsX2+rX3一rwhs=0.法平面方程(平面法向为V1(s))为一rsinωs(X1一rcosωs)+rcosωs(X2一rsin ωs)+h(X3一ωhs)=0即 一rsinωsX1+rcosωsX2+hX3一ωh2s=0.
由例1.1.3,知V1(s)=x'(s)=w(-rsin(ws,rcosws,h)(切向量,s为弧长),且k(s)V2(s)一V1'(s)=ω2(一rcosωs,一rsinωs,0),V2(s)=一(cosωs,sinωs,0),切线方程(方向为V1(s))为主法线方程(方向为V2(s))为密切平面方程(平面法向为V3(s))为hsinωs(X1一rcosωs)一hcosωs(X2一rsincos)+r(X3一ωhs)=0,即hsinωsX1一hcosωsX2+rX3一rwhs=0.法平面方程(平面法向为V1(s))为一rsinωs(X1一rcosωs)+rcosωs(X2一rsinωs)+h(X3一ωhs)=0,即一rsinωsX1+rcosωsX2+hX3一ωh2s=0.
相似问题
求悬链面M:求曲面M:F(x y z)=0的渐近曲线应满足的方程.求曲面M:F(x y z)=0的渐
求悬链面M:求曲面M:F(x,y,z)=0的渐近曲线应满足的方程.求曲面M:F(x,y,z)=0的渐近曲线应满足的方程.请帮忙给出正确答案和分析,谢谢!
求螺旋面x(u v)=(ucosv usinv u+v)的Gauss(总)曲率KG与平均曲率H.请帮
求螺旋面x(u,v)=(ucosv,usinv,u+v)的Gauss(总)曲率KG与平均曲率H.请帮忙给出正确答案和分析,谢谢!
求u曲线与v曲线的正交轨线的微分方程.请帮忙给出正确答案和分析 谢谢!
求u曲线与v曲线的正交轨线的微分方程.请帮忙给出正确答案和分析,谢谢!
若R3中曲面的所有曲线均为曲率线 则它为全脐的曲面.进而 若该曲面连通 则它为球面片或平面片.(参阅
若R3中曲面的所有曲线均为曲率线,则它为全脐的曲面.进而,若该曲面连通,则它为球面片或平面片.(参阅引理3.1.4.)请帮忙给出正确答案和分析,谢谢!
设曲面M上的一条曲率线C:x(s)(s为弧长) 它的每一点处的从法向量V3(s)与曲面在该点处的法向
设曲面M上的一条曲率线C:x(s)(s为弧长),它的每一点处的从法向量V3(s)与曲面在该点处的法向量n(s)成定角,且V3(s) n(s)≠±1(即V3s(s)不平行于n(s)).证












