设P0为两曲线x(s)与给定一个中心在m 半径为r>0的球面.设S为曲线C:x(s)的弧长 令f(s
设P0为两曲线x(s)与给定一个中心在m、半径为r>0的球面.设S为曲线C:x(s)的弧长,令f(s)一Ex(s)一
给定一个中心在m、半径为r>0的球面.设S为曲线C:x(s)的弧长,令f(s)一Ex(s)一m]2一r2.如果在s0满足下列条件:f(0)(s0)=f(s0)=[x(s0)一m]2一r2=0 (r为常数),f(s0)=f(s0)=…=f(n)(s0)=0,则称曲线x(s)与已给球面有n阶接触.证明:(1)如果C∞曲线x(s)落在已给球面上,则曲线x(s)与球面有任意阶接触;(2)如果τ(s0)=0,则曲线x(s)在x(s0)与某一球面有3阶接触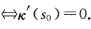 .从而,平面连通曲线不能与球面处处有3阶接触,除非曲线本身属于球面的一个圆.
.从而,平面连通曲线不能与球面处处有3阶接触,除非曲线本身属于球面的一个圆.
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(1)由于C∞曲线x(s)落在已给球面上故f(s)=[x(s)一m2一r2≡0(r为常数);且对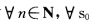 有f'(s0)=f''(s0)=…=f(n)(s0).因此x(s)在s0处有n阶接触.由于n和s0任取所以x(s)与该球面有任意阶接触.(2)(→)设曲线x(s)在x(s0)点处与某球面有3阶接触则f(0)(s0)=f(s0)=f'(s0)=f''(s0)=f'''(s0)=0其中
有f'(s0)=f''(s0)=…=f(n)(s0).因此x(s)在s0处有n阶接触.由于n和s0任取所以x(s)与该球面有任意阶接触.(2)(→)设曲线x(s)在x(s0)点处与某球面有3阶接触则f(0)(s0)=f(s0)=f'(s0)=f''(s0)=f'''(s0)=0其中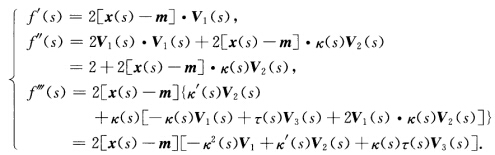 根据f(s0)=0τ(s0)=0有0=f'''(s0)=2[x(s0)一m.k'(s0)V2(s0).显然0=f''(s0)=2+2[x(s0)一mk(s0)V2(s0)蕴涵着[x(s0)一mV2(s0)≠0.从上式并结合前面f'''(s0)=0的式子推得K'(s0)=0.(←)若τ(s0)=0k'(s0)=0又k(s0)>0作以
根据f(s0)=0τ(s0)=0有0=f'''(s0)=2[x(s0)一m.k'(s0)V2(s0).显然0=f''(s0)=2+2[x(s0)一mk(s0)V2(s0)蕴涵着[x(s0)一mV2(s0)≠0.从上式并结合前面f'''(s0)=0的式子推得K'(s0)=0.(←)若τ(s0)=0k'(s0)=0又k(s0)>0作以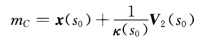 为中心
为中心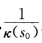 为半径的球面则
为半径的球面则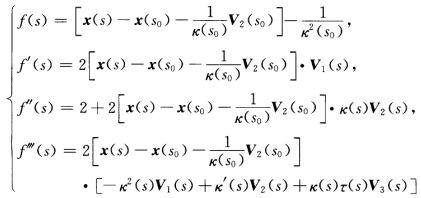
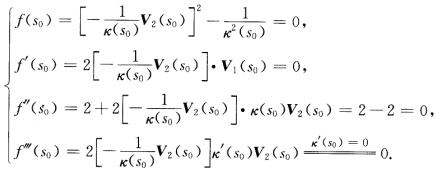 这表明x(s)在x(s0)与球面
这表明x(s)在x(s0)与球面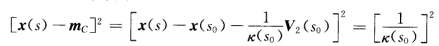 有3阶接触.最后如果平面曲线(r(s)≡0)x(s)与球面(x—m)2=r2(对不同的s球面可不相同)处处有3阶接触根据上述有k'(s)≡0即k(s)=k(s0)(常数).再根据推论1.5.2知曲线x(s)为一个圆当然它属于某个(实际上是无穷多个)球面上的圆.如果平面曲线(τ(s)≡0)x(s)与一个固定的球面(x—m)2=r2处处有3阶接触当然它为平面与固定球面的交线不需证明x(s)必为该球面上的一个圆.
有3阶接触.最后如果平面曲线(r(s)≡0)x(s)与球面(x—m)2=r2(对不同的s球面可不相同)处处有3阶接触根据上述有k'(s)≡0即k(s)=k(s0)(常数).再根据推论1.5.2知曲线x(s)为一个圆当然它属于某个(实际上是无穷多个)球面上的圆.如果平面曲线(τ(s)≡0)x(s)与一个固定的球面(x—m)2=r2处处有3阶接触当然它为平面与固定球面的交线不需证明x(s)必为该球面上的一个圆.
(1)由于C∞曲线x(s)落在已给球面上,故f(s)=[x(s)一m2一r2≡0(r为常数);且对,有f'(s0)=f''(s0)=…=f(n)(s0).因此,x(s)在s0处有n阶接触.由于n和s0任取,所以x(s)与该球面有任意阶接触.(2)(→)设曲线x(s)在x(s0)点处与某球面有3阶接触,则f(0)(s0)=f(s0)=f'(s0)=f''(s0)=f'''(s0)=0,其中根据f(s0)=0,τ(s0)=0,有0=f'''(s0)=2[x(s0)一m.k'(s0)V2(s0).显然,0=f''(s0)=2+2[x(s0)一m,k(s0)V2(s0)蕴涵着[x(s0)一mV2(s0)≠0.从上式并结合前面f'''(s0)=0的式子,推得K'(s0)=0.(←)若τ(s0)=0,k'(s0)=0,又k(s0)>0,作以为中心为半径的球面,则这表明,x(s)在x(s0)与球面有3阶接触.最后,如果平面曲线(r(s)≡0)x(s)与球面(x—m)2=r2(对不同的s,球面可不相同)处处有3阶接触,根据上述,有k'(s)≡0,即k(s)=k(s0)(常数).再根据推论1.5.2知,曲线x(s)为一个圆,当然它属于某个(实际上是无穷多个)球面上的圆.如果平面曲线(τ(s)≡0)x(s)与一个固定的球面(x—m)2=r2处处有3阶接触,当然,它为平面与固定球面的交线,不需证明,x(s)必为该球面上的一个圆.
相似问题
求圆柱螺线的切向量 切线 主法线 密切平面 法平面方程.请帮忙给出正确答案和分析 谢谢!
求圆柱螺线的切向量、切线、主法线、密切平面、法平面方程.请帮忙给出正确答案和分析,谢谢!
求悬链面M:求曲面M:F(x y z)=0的渐近曲线应满足的方程.求曲面M:F(x y z)=0的渐
求悬链面M:求曲面M:F(x,y,z)=0的渐近曲线应满足的方程.求曲面M:F(x,y,z)=0的渐近曲线应满足的方程.请帮忙给出正确答案和分析,谢谢!
求螺旋面x(u v)=(ucosv usinv u+v)的Gauss(总)曲率KG与平均曲率H.请帮
求螺旋面x(u,v)=(ucosv,usinv,u+v)的Gauss(总)曲率KG与平均曲率H.请帮忙给出正确答案和分析,谢谢!
求u曲线与v曲线的正交轨线的微分方程.请帮忙给出正确答案和分析 谢谢!
求u曲线与v曲线的正交轨线的微分方程.请帮忙给出正确答案和分析,谢谢!
若R3中曲面的所有曲线均为曲率线 则它为全脐的曲面.进而 若该曲面连通 则它为球面片或平面片.(参阅
若R3中曲面的所有曲线均为曲率线,则它为全脐的曲面.进而,若该曲面连通,则它为球面片或平面片.(参阅引理3.1.4.)请帮忙给出正确答案和分析,谢谢!












