若R3中曲面的所有曲线均为曲率线 则它为全脐的曲面．进而 若该曲面连通 则它为球面片或平面片．(参阅
若R3中曲面的所有曲线均为曲率线，则它为全脐的曲面．进而，若该曲面连通，则它为球面片或平面片．(参阅引理3．1．4．)
请帮忙给出正确答案和分析，谢谢！
参考解答
481***102
2024-11-17 02:39:43
正确答案：曲面的所有曲线为曲率线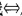
所有的方向du：dv都满足曲率线方程：
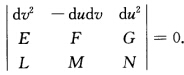它等价于(LMN)=λ(EFG) (即曲面是全脐的)．事实上(←)由行列式性质推得．(→)取du：dv=1：0代入上面的行列式得
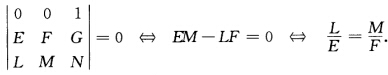再取du：dv=0：1代入上面的行列式得
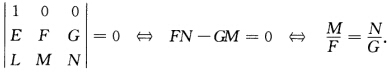综合上述有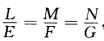
即(LMN)=λ(EFG)．
曲面的所有曲线为曲率线所有的方向du：dv都满足曲率线方程：它等价于(L,M,N)=λ(E,F,G)(即曲面是全脐的)．事实上,(←)由行列式性质推得．(→)取du：dv=1：0,代入上面的行列式,得再取du：dv=0：1,代入上面的行列式,得综合上述,有即(L,M,N)=λ(E,F,G)．
相似问题
设曲面M上的一条曲率线C：x(s)(s为弧长) 它的每一点处的从法向量V3(s)与曲面在该点处的法向
设曲面M上的一条曲率线C：x(s)(s为弧长)，它的每一点处的从法向量V3(s)与曲面在该点处的法向量n(s)成定角，且V3(s) n(s)≠±1(即V3s(s)不平行于n(s))．证
设曲面M1 M2的交线C的曲率为k 曲线C在Mi上的法曲率为kni(i=1 2) M1与M2的法线交
设曲面M1，M2的交线C的曲率为k，曲线C在Mi上的法曲率为kni(i=1，2)，M1与M2的法线交角为θ证明：k2sin2θ=kn12+kn22一2kn1kn2cosθ．请帮忙给出正确答案和分析，谢谢！
求正螺面x(u v)=(vcosu vsinu an) (a>0)上的测地线．请帮忙给出正确答案和分
求正螺面x(u，v)=(vcosu，vsinu，an) (a>0)上的测地线．请帮忙给出正确答案和分析，谢谢！
设圆柱螺线 设x(t)(an中的C1正则曲线 x(t0)为定点P0到该曲线距离最近的点．证明：切向量
设圆柱螺线 设x(t)(an中的C1正则曲线，x(t0)为定点P0到该曲线距离最近的点．证明：切向量x(t0)与x(设x(t)(an中的C1正则曲线，x(t0)为定点P0到该曲线距离
两条C3曲线证明：曲线为球面曲线证明：曲线为球面曲线请帮忙给出正确答案和分析 谢谢！
两条C3曲线证明：曲线为球面曲线证明：曲线为球面曲线请帮忙给出正确答案和分析，谢谢！
