设曲面M上的一条曲率线C：x(s)(s为弧长) 它的每一点处的从法向量V3(s)与曲面在该点处的法向
设曲面M上的一条曲率线C：x(s)(s为弧长)，它的每一点处的从法向量V3(s)与曲面在该点处的法向量n(s)成定角，且V3(s).n(s)≠±1(即V3s(s)不平行于n(s))．证明：C为平面曲线．
请帮忙给出正确答案和分析，谢谢！
参考解答
456***102
2024-11-17 02:43:03
正确答案：因为V3(s).n(s)=cosθ=c (常数)所以两边对s求导得到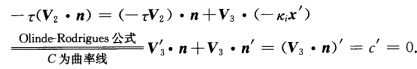
又因为V3和n不平行所以V2.n≠0．它蕴涵τ=0．根据定理1．2．2C为平面曲线．
因为V3(s).n(s)=cosθ=c(常数),所以两边对s求导,得到又因为V3和n不平行,所以V2.n≠0．它蕴涵τ=0．根据定理1．2．2,C为平面曲线．
相似问题
设曲面M1 M2的交线C的曲率为k 曲线C在Mi上的法曲率为kni(i=1 2) M1与M2的法线交
设曲面M1，M2的交线C的曲率为k，曲线C在Mi上的法曲率为kni(i=1，2)，M1与M2的法线交角为θ证明：k2sin2θ=kn12+kn22一2kn1kn2cosθ．请帮忙给出正确答案和分析，谢谢！
求正螺面x(u v)=(vcosu vsinu an) (a>0)上的测地线．请帮忙给出正确答案和分
求正螺面x(u，v)=(vcosu，vsinu，an) (a>0)上的测地线．请帮忙给出正确答案和分析，谢谢！
设圆柱螺线 设x(t)(an中的C1正则曲线 x(t0)为定点P0到该曲线距离最近的点．证明：切向量
设圆柱螺线 设x(t)(an中的C1正则曲线，x(t0)为定点P0到该曲线距离最近的点．证明：切向量x(t0)与x(设x(t)(an中的C1正则曲线，x(t0)为定点P0到该曲线距离
两条C3曲线证明：曲线为球面曲线证明：曲线为球面曲线请帮忙给出正确答案和分析 谢谢！
两条C3曲线证明：曲线为球面曲线证明：曲线为球面曲线请帮忙给出正确答案和分析，谢谢！
设曲面M的第3基本形式为Ⅲ=edu2+2fdudv+gdv2． 证明： (1) (2)(LN一M2)
设曲面M的第3基本形式为Ⅲ=edu2+2fdudv+gdv2． 证明： (1) (2)(LN一M2)2=(EG—F2)(eg一f2)．请帮忙给出正确答案和分析，谢谢！
