对R3中定向光滑的2维闭曲面M 如果(Minkowski公式)设MCR3为2维光滑 定向 紧致曲面
对R3中定向光滑的2维闭曲面M,如果(Minkowski公式)设MCR3为2维光滑、定向、紧致曲面,x(P)为它的位置
(Minkowski公式)设MCR3为2维光滑、定向、紧致曲面,x(P)为它的位置向量,n(P)为P点处的连续单位法向量.函数φ(P)=一=一x(P)n(P) (P∈M)称为曲面M的支撑函数.它是坐标原点O到P的切平面的有向距离,则有Minkowski公式: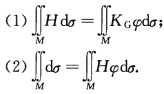
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:(dxe3de3)+(xde3de3)+(xe3dde3)=(ω1e1一ω2e2e3ω31e1+ω32e2)+(xω31e1+ω32e2ω31e1+ω32e2)+(xe30)=(一ω1∧ω32+ω2∧ω31)+2ω31∧ω32(xe1e2)+0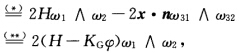 其中(**)dω12=ω13∧ω32=一KGω1∧ω2参阅例2.11.1而(*)一ω1∧ω32+ω32∧ω31=2Hω1∧ω2证明如下:一ω1∧ω32+ω2∧ω31=一(ω1∧(一h21ω1一h22ω2)+ω2∧(一h11ω1一ω12ω2)=(h22+h11)ω1∧ω2=2Hω1∧ω2.或者选取正交参数系{uv(参阅例2.11.1)有
其中(**)dω12=ω13∧ω32=一KGω1∧ω2参阅例2.11.1而(*)一ω1∧ω32+ω32∧ω31=2Hω1∧ω2证明如下:一ω1∧ω32+ω2∧ω31=一(ω1∧(一h21ω1一h22ω2)+ω2∧(一h11ω1一ω12ω2)=(h22+h11)ω1∧ω2=2Hω1∧ω2.或者选取正交参数系{uv(参阅例2.11.1)有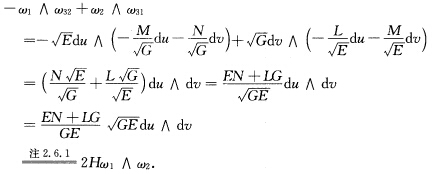 对d(xndn)=2(H—KGφ)ω1∧ω2两边积分就得到
对d(xndn)=2(H—KGφ)ω1∧ω2两边积分就得到 即
即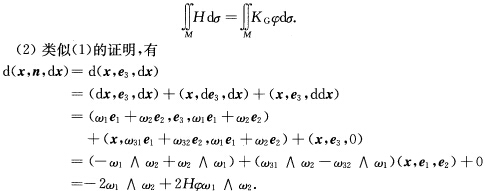 两边积分就得到
两边积分就得到 作为Minkowski公式的应用我们给出两个有关球面特性的定理.
作为Minkowski公式的应用我们给出两个有关球面特性的定理.
(dx,e3,de3)+(x,de3,de3)+(x,e3,dde3)=(ω1e1一ω2e2,e3,ω31e1+ω32e2)+(x,ω31e1+ω32e2,ω31e1+ω32e2)+(x,e3,0)=(一ω1∧ω32+ω2∧ω31)+2ω31∧ω32(x,e1,e2)+0其中(**)dω12=ω13∧ω32=一KGω1∧ω2,参阅例2.11.1,而(*)一ω1∧ω32+ω32∧ω31=2Hω1∧ω2,证明如下:一ω1∧ω32+ω2∧ω31=一(ω1∧(一h21ω1一h22ω2)+ω2∧(一h11ω1一ω12ω2)=(h22+h11)ω1∧ω2=2Hω1∧ω2.或者选取正交参数系{u,v(参阅例2.11.1),有对d(x,n,dn)=2(H—KGφ)ω1∧ω2两边积分,就得到即两边积分就得到作为Minkowski公式的应用,我们给出两个有关球面特性的定理.
相似问题
证明:双益抛物线(马鞍面)M:x(u v)=(a(u+v) b(u一v) 2uv) (a>0 b>0
证明:双益抛物线(马鞍面)M:x(u,v)=(a(u+v),b(u一v),2uv) (a>0,b>0)不是可展曲面.请帮忙给出正确答案和分析,谢谢!
设曲面M的第1基本形式取等温形式:I=ρ2(du2+dv2).证明:其中从而 当一时 KG=4c(常
设曲面M的第1基本形式取等温形式:I=ρ2(du2+dv2).证明:其中从而,当一时,KG=4c(常数).请帮忙给出正确答案和分析,谢谢!
求悬链面M:求曲面z=xy2的渐近线.求曲面z=xy2的渐近线.请帮忙给出正确答案和分析 谢谢!
求悬链面M:求曲面z=xy2的渐近线.求曲面z=xy2的渐近线.请帮忙给出正确答案和分析,谢谢!
若曲面M的参数曲线所构成的四边形对边长相等 则称它为Chebyshev网. (1)参数曲线构成Che
若曲面M的参数曲线所构成的四边形对边长相等,则称它为Chebyshev网. (1)参数曲线构成Chebyshev网Ev=Gu=0. (2)参数曲线构成Chebyshev网时,可取新参数
对R3中定向光滑的2维闭曲面M 如果设为KG>0的2维紧致 定向 连通的曲面 且 则M为球面.设为K
对R3中定向光滑的2维闭曲面M,如果设为KG>0的2维紧致、定向、连通的曲面,且,则M为球面.设为KG>0的2维紧致、定向、连通的曲面,且,则M为球面.请帮忙












