对R3中定向光滑的2维闭曲面M 如果设为KG>0的2维紧致 定向 连通的曲面 且 则M为球面．设为K
对R3中定向光滑的2维闭曲面M，如果设为KG>0的2维紧致、定向、连通的曲面，且，则M为球面．
设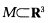
为KG>0的2维紧致、定向、连通的曲面，且
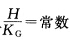，则M为球面．
请帮忙给出正确答案和分析，谢谢！
参考解答
432***102
2024-11-16 22:16:11
正确答案：因为
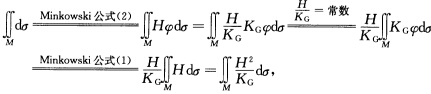移项得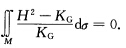
因为KG>0与H2一KG连续以及
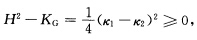所以应用反证法立知H2一KG=0即k1=k2M为全脐点曲面．根据定理3．1．1KG>0的紧致、定向、连通曲面M必为整个球面．
因为移项得因为KG>0与H2一KG连续,以及所以应用反证法立知H2一KG=0,即k1=k2,M为全脐点曲面．根据定理3．1．1,KG>0的紧致、定向、连通曲面M必为整个球面．
相似问题
设三个函数x(u v) y(u v) z(u v)为微分方程：的独立解 且x2+y2+z2也为方程的
设三个函数x(u，v)，y(u，v)，z(u，v)为微分方程：的独立解，且x2+y2+z2也为方程的解．证明：曲面x(u，v)=(x(u，v)，y(u，v)，z(u，v))的参数曲线为曲率
设x(t)为平面曲线 相对曲率为kr(t) 求 的相对曲率．请帮忙给出正确答案和分析 谢谢！
设x(t)为平面曲线，相对曲率为kr(t)，求 的相对曲率．请帮忙给出正确答案和分析，谢谢！
设s为弧长 在R3中证明：kτ=V1.V3．请帮忙给出正确答案和分析 谢谢！
设s为弧长，在R3中证明：kτ=V1 V3．请帮忙给出正确答案和分析，谢谢！
当Aδu+Bδv=0时 C的正交轨线的微分方程．设曲面M.的第1基本形式为I.=D.U2+(U2+A
当Aδu+Bδv=0时，C的正交轨线的微分方程．设曲面M 的第1基本形式为I =D U2+(U2+A 2)D V2 (A &G T;0) 求：请帮忙给出正确答案和分析，谢谢！
对R3中定向光滑的2维闭曲面M 如果设为2维紧致 定向 连通的凸曲面 且M的平均曲率H=常数 则M为
对R3中定向光滑的2维闭曲面M，如果设为2维紧致、定向、连通的凸曲面，且M的平均曲率H=常数，则M为一个设为2维紧致、定向、连通的凸曲面，且M的平均曲率H=
