对R3中定向光滑的2维闭曲面M 如果设为2维紧致 定向 连通的凸曲面 且M的平均曲率H=常数 则M为
对R3中定向光滑的2维闭曲面M,如果设为2维紧致、定向、连通的凸曲面,且M的平均曲率H=常数,则M为一个
设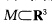 为2维紧致、定向、连通的凸曲面,且M的平均曲率H=常数,则M为一个球面;
为2维紧致、定向、连通的凸曲面,且M的平均曲率H=常数,则M为一个球面;
请帮忙给出正确答案和分析,谢谢!
参考解答
正确答案:因为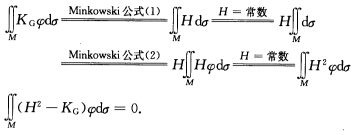 此外由于
此外由于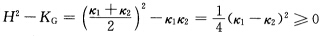 以及M为凸曲面可将坐标原点取在凸曲面所包围的开区域内并取单位法向n指向凸曲面包围的开区域(n为单位内法向量).此时φ>0.因此
以及M为凸曲面可将坐标原点取在凸曲面所包围的开区域内并取单位法向n指向凸曲面包围的开区域(n为单位内法向量).此时φ>0.因此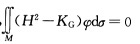 =0蕴涵着H2一KG=0(应用反证法并注意到H2一KG≥0及H2一KG为连续函数)则H2=KG.根据上述不等式有
=0蕴涵着H2一KG=0(应用反证法并注意到H2一KG≥0及H2一KG为连续函数)则H2=KG.根据上述不等式有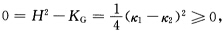 k1一k2=0 k1=k2即M为全脐点曲面.根据定理3.1.1紧致、定向、连通曲面M必为整个球面.
k1一k2=0 k1=k2即M为全脐点曲面.根据定理3.1.1紧致、定向、连通曲面M必为整个球面.
因为此外,由于以及M为凸曲面,可将坐标原点取在凸曲面所包围的开区域内,并取单位法向n指向凸曲面包围的开区域(n为单位内法向量).此时,φ>0.因此,=0蕴涵着H2一KG=0(应用反证法,并注意到H2一KG≥0及H2一KG为连续函数),则H2=KG.根据上述不等式,有k1一k2=0,k1=k2,即M为全脐点曲面.根据定理3.1.1,紧致、定向、连通曲面M必为整个球面.
相似问题
设圆柱螺线 请帮忙给出正确答案和分析 谢谢!
设圆柱螺线 请帮忙给出正确答案和分析,谢谢!
求旋轮线(摆线)x(t)=a(t—sin t 1一cost) (a>0)的渐缩线y(t).请帮忙给出
求旋轮线(摆线)x(t)=a(t—sin t,1一cost) (a>0)的渐缩线y(t).请帮忙给出正确答案和分析,谢谢!
若k为u曲线的曲率 则请帮忙给出正确答案和分析 谢谢!
若k为u曲线的曲率,则请帮忙给出正确答案和分析,谢谢!
设曲面M的第3基本形式为Ⅲ=edu2+2fdudv+gdv2. 证明: (1)设以z轴为旋转轴的旋转
设曲面M的第3基本形式为Ⅲ=edu2+2fdudv+gdv2. 证明: (1)设以z轴为旋转轴的旋转曲面M的经线有水设以z轴为旋转轴的旋转曲面M的经线有水平切线.证明
求曲面x(u v)=(u3 v3 u+v)的抛物点轨迹.请帮忙给出正确答案和分析 谢谢!
求曲面x(u,v)=(u3,v3,u+v)的抛物点轨迹.请帮忙给出正确答案和分析,谢谢!












